以下统计图描述了九年级(1)班学生在为期一个月的读书月活动中，三个阶段(上旬、中旬、 下旬)日人均阅读时间的情况：
(1)从统计图可知，九年级(1)班共有学生多少人?
(2)求图22．1中a的值
(3)从图22-1、22-2 中判断，在这次读书月活动中，该班学生每日阅读时间_______(填“普遍增加了”或“普遍减少了”)：
(4)通过这次读书月活动，如果该班学生初步形成了良好的每日阅读习惯，参照以上统计图的变化趋势，至读书月活动结束时，该班学生日人均阅读时间在0．5～1(即0．5≤t<10)小 时的人数比活动开展初期增加了多少人?
频数（学生人数） 活动上旬频数分布直方图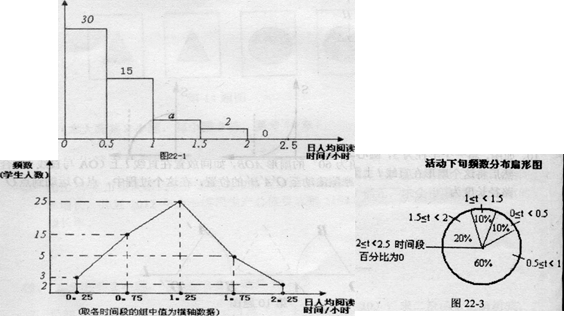
(每个小矩形含左端点，不含右端点)
已知一次函数物图象经过A（﹣2，﹣3），B（1，3）两点．
（1）求这个一次函数的解析式；
（2）试判断点P（﹣1，1）是否在这个一次函数的图象上．
如图，把△OAB放置于平面直角坐标系xOy中，∠OAB=90°，OA=2，AB=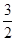
，把△OAB沿x轴的负方向平移2OA的长度后得到△DCE．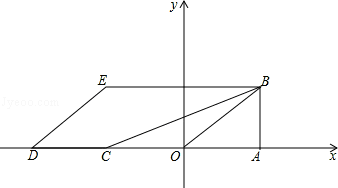
（1）若过原点的抛物线y=ax2+bx+c经过点B、E，求此抛物线的解析式；
（2）若点P在该抛物线上移动，当点p在第一象限内时，过点p作PQ⊥x轴于点Q，连接OP．若以O、P、Q为定点的三角形与以B、C、E为定点的三角形相似，直接写出点P的坐标；
（3）若点M（﹣4，n）在该抛物线上，平移抛物线，记平移后点M的对应点为M′，点B的对应点为B′．当抛物线向左或向右平移时，是否存在某个位置，使四边形M′B′CD的周长最短？若存在，求出此时抛物线的解析式；若不存在，请说明理由．
东方专卖店专销某种品牌的钢笔，进价12元/支，售价20元/支．为了促销，专卖店决定凡是买10支以上的，每多买一支，售价就降低0．10元（例如，某人买20支钢笔，于是每只降价0．10×=1元，就可以按19元/支的价格购买），但是最低价为16元/支．
（1）求顾客一次至少买多少支，才能以最低价购买？
（2）写出当一次购买x支时（x＞10），利润y（元）与购买量x（支）之间的函数关系式；
（3）有一天，一位顾客买了46支，另一位顾客买了50支，专卖店发现卖了50支反而比卖46支赚的钱少，为了使每次卖的多赚钱也多，在其他促销条件不变的情况下，最低价16元/支至少要提高到多少，为什么？
如图，在▱ABCD中，过A、C、D三点的⊙O交AB于点E，连接DE、CE，∠CDE=∠BCE．
（1）求证：AD=CE；
（2）判断直线BC与⊙O的位置关系，并说明理由；
（3）若BC=3，DE=6，求BE的长．
在平面直角坐标系xOy中，对于任意三点A、B、C的“矩面积”，给出如下定义：“水平底”a：任意两点横坐标差的最大值，“铅垂高”h：任意两点纵坐标差的最大值，则“矩面积”S=ah．
例如：三点坐标分别为A（1，2），B（﹣3，1），C（2，﹣2），则“水平底”a=5，“铅垂高”h=4，“矩面积”S=ah=20．
（1）已知点A（1，2），B（﹣3，1），P（0，t）．
①若A、B、P三点的“矩面积”为12，求点P的坐标；
②A、B、P三点的“矩面积”的最小值为．
（2）已知点E（4，0），F（0，2）M（m，4m），其中m＞0．若E、F、M三点的“矩面积”的为8，求m的取值范围．