如图所示，两平行金属板A、B长度l=0.8m，间距d=0.6m．直流电源E能提供的电压足够大，位于极板左侧中央的粒子源可以沿水平方向向右连续发射比荷为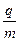
=l
×107C/kg、重力不计的带电粒子，射入板间的粒子速度均为v0=4×106m/s．在极板右侧有一个垂直纸面向里的匀强磁场，磁感应强度B=lT，分布在环带区域中，该环带的内外圆的圆心与两板间的中心重合于O点，环带的内圆半径Rl=
m．将变阻器滑动头由a向b慢慢滑动，改变两板间的电压时，带电粒子均能从不同位置穿出极板射向右侧磁场．
（1）问从板间右侧射出的粒子速度的最大值vm是多少?
（2）若粒子射出电场时，速度的反向延长线与v0所在直线交于O/点，试证明O/点与极板右端边缘的水平距离x=
，即O/与O重合，所有粒子都好像从两板的中心射出一样．
（3）为使粒子不从磁场右侧穿出，求环带磁场的最小宽度d．
额定功率为80 kW的汽车，在平直的公路上行驶的最大速度是20 m/s，汽车的质量是2 t，如果汽车从静止开始做匀加速直线运动，加速度的大小是2 m/s2，运动过程中阻力不变，求：
(1)汽车受到的阻力多大？
(2)3 s末汽车的瞬时功率多大？
(3)汽车维持匀加速运动的时间是多少？
质量为3 kg的物体，从高30 m处自由落下，(g取10 m/s2)问：
(1)第2 s内重力做功的功率是多少？
(2)第2 s末重力做功的功率是多少？
一位排球运动员，体重70 kg，身高1.80 m，静止站立时伸直手臂摸到的最大高度为2.30 m，跳起来能摸到的最大高度为3.30 m，起跳过程时间为0.4 s，那么他起跳时做的功为多少？起跳过程中的平均功率约为多大？(g取10 m/s2)
一个质量为2 kg的物块，沿倾角为37°的光滑斜面由静止开始下滑，g取10 m/s2，斜面足够长．求：
(1)物块下滑4 s时重力的瞬时功率；
(2)在这4 s内重力的平均功率．
一个质量m＝2 kg的物体，受到与水平方向成37°角斜向上方的拉力F1＝10 N，在水平
地面上移动的距离l＝2 m．物体与地面间的滑动摩擦力F2＝4.2 N，求外力对物体所做的
总功．(如图所示)