学校准备从5位报名同学中挑选3人,分别担任2011年世界大学生运动会田径、游泳和球类3个不同项目比赛的志愿者,已知其中同学甲不能担任游泳比赛的志愿者,则不同的安排方法共有
| A.24种 | B.36种 | C.48种 | D.60种 |
如图,在等腰梯形SBCD中,AB∥CD,且AB=2AD, 设
设 ,以A,B为焦点且过点D的双曲线离
,以A,B为焦点且过点D的双曲线离 心率为
心率为 ,以C,D为焦点且过点A的椭圆的离心率为
,以C,D为焦点且过点A的椭圆的离心率为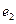 ,则()
,则()
A.随着 角的增大 角的增大 , , 增大, 增大, 也增大 也增大 |
B.随着 角的增大, 角的增大, 减小, 减小, 为定值 为定值 |
C.随着 角的增大, 角的增大, 增大, 增大, 为定值 为定值 |
D.随着 角的增大, 角的增大, 减小, 减小,  也减小 也减小 |
已知点 是
是 的重心,
的重心,
 若
若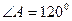 ,
, ,则
,则 的最小值是()
的最小值是()
A. |
B.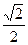 |
C. |
D. |
三棱锥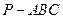 中,
中, ,
, 是等腰直角三角形,
是等腰直角三角形, .若
.若 为
为 中点,则
中点,则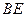 与平面
与平面 所成的角的大小等于( )
所成的角的大小等于( )
A.
 B.
B.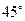 C
C  D.
D.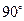
如图示,已知直线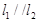 ,点A是
,点A是 之间的一个定点,且A到
之间的一个定点,且A到 的距离分别为4、3,点B是直线
的距离分别为4、3,点B是直线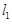 上的动点,若
上的动点,若 与直线
与直线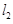 交于点C,则
交于点C,则 面积的最小值为()
面积的最小值为()
| A.12 | B.6 | C.3 | D.18 |
设e<x<10,记a=ln(lnx),b=lg(lgx),c=ln(lgx),d=lg(lnx),则a,b,c,d的大小关系()
| A.c<b<d<a | B.c<d<a<b | C.a<b< c<d c<d |
D.b<d<c<a |