如图所示的矩形包书纸中,虚线是折痕,阴影是裁剪掉的部分,四个角均为大小相同的正方形,正方形的边长为折叠进去的宽度.
(1)设课本的长为a cm,宽为b cm,厚为c cm,如果按如图所示的包书方式,将封面和封底各折进去3cm,用含a,b,c的代数式,分别表示满足要求的矩形包书纸的长与宽;
(2)现有一本长为19cm,宽为16cm,厚为6cm的字典,你能用一张长为43cm,宽为26cm的矩形 纸,按图所示的方法包好这本字典,并使折叠进去的宽度不小于3cm吗?请说明理由.
纸,按图所示的方法包好这本字典,并使折叠进去的宽度不小于3cm吗?请说明理由.
某商店第一次用6000元购进了练习本若干本,第二次又用6000元购进该款练习本,但这次每本进货的价格是第一次进货价格的1.2倍,购进数量比第一次少了1000本.
(1)问:第一次每本的进货价是多少元?
(2)若要求这两次购进的练习本按同一价格全部销售完毕后获利不低于4500元,问每本售价至少是多少元?
如图,在△ABC中,AD是角平分钱,点E在AC上,且∠EAD=∠ADE.
(1)求证:△DCE∽△BCA;
(2)若AB=3,AC=4.求DE的长.
在一个布口袋里装着白、红、黑三种颜色的小球,它们除颜色之外没有任何其它区别,其中有白球3只、红球2只、黑球1只.袋中的球已经搅匀.
(1)闭上眼睛随机地从袋中取出1只球,求取出的球是黑球的概率;
(2)若取出的第1只球是红球,将它放在桌上,闭上眼睛从袋中余下的球中再随机地取出1只球,这时取出的球还是红球的概率是多少?
(3)若取出一只球,将它放回袋中,闭上眼睛从袋中再随机地取出1只球,两次取出的球都是白球概率是多少?(用列表法或树状图法计算)
解方程: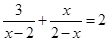 .
.
化简或求值
(1)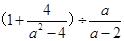
(2)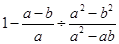 ,其中a=﹣
,其中a=﹣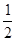 ,b=1.
,b=1.