设函数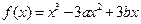 的图像与直线
的图像与直线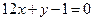 相切于点(1,-11)
相切于点(1,-11)
(Ⅰ)求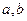 的值;
的值;
(Ⅱ)讨论函数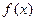 的单调性。
的单调性。
已知命题 :方程
:方程 有两个不等的负实根;命题
有两个不等的负实根;命题 :方程
:方程 无实根, 若“
无实根, 若“ 或
或 ”为真,而“
”为真,而“ 且
且 ”为假,求实数
”为假,求实数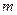 的取值范围.
的取值范围.
某体育彩票规定:从01至36个号中抽出7个号为一注,每注2元,某人想从01至10中选3个连续的号,从11至20中选2个连续的号,从21至30中选1个号,从31至36中选1个号组成一注,此人想把这种特殊要求的号买全,至少要花多少钱?
某城市有甲、乙、丙、丁四个城区,分布如图1-1-3所示,现用五种不同的颜色涂在该城市地图上,要求相邻区域的颜色不相同,不同的涂色方案共有多少种?
有0,1,2,3,…,8这9个数字,用这9个数字组成四位的密码,共可组成多少个这样的密码?
如图所示:小圆圈表示网络的结点,结点之间的连线表示它们有网络联系,连线上标注的数字表示该段网线单位时间内可以通过的最大信息量,现从结点A向结点B传递信息,信息可以分开沿不同路线同时传递,求单位时间内传递的最大信息量.