甲打靶射击，有4发子弹，其中有一发是空弹.
（1）求空弹出现在第一枪的概率；
（2）求空弹出现在前三枪的概率;
（3）如果把空弹换成实弹，甲前三枪在靶上留下三个两两距离分别为3，4，5的弹孔
，第四枪瞄准了三角形
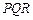射击,第四个弹孔落在三角形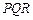内
，求第四个弹孔与前三个弹孔的距离都超过1的概率（忽略弹孔大小）.
已知圆
，M是圆C上的动点，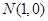
，MN的垂直平分线交CM于点P,求点P的轨迹方程．
已知函数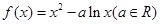
（1）若
，求函数
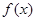的极值；
（2）已知函数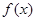在点
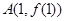处的切线为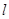
，若此切线在点A处穿过
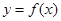的图像（即函数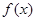上的动点P在点A附近沿曲线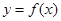运动，经过点A时从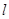的一侧进入另一侧），求函数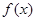的表达式；
（3）若
，函数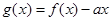
有且仅有一个零点，求实数
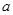的值．
已知椭圆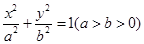
，F为椭圆的右焦点，点A,B分别为椭圆的上下顶点，过点B作AF的垂线，垂足为M．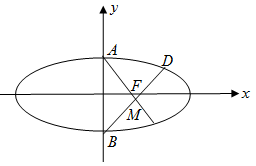
（1）若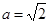
，
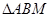的面积为1，求椭圆方程；
（2）是否存在椭圆，使得点B关于直线AF对称的点D仍在椭圆上，若存在，求椭圆的离心率的值；若不存在，说明理由．
如图，地图上有一竖直放置的圆形标志物，圆心为C，与地面的接触点为G．与圆形标志物在同一平面内的地面上点P处有一个观测点，且PG=50m．在观测点正前方10m处（即PD=10m）有一个高位10m（即ED=10m）的广告牌遮住了视线，因此在观测点所能看到的圆形标志的最大部分即为图中从A到F的圆弧．
（1）若圆形标志物半径为25m，以PG所在直线为X轴，G为坐标原点，建立直角坐标系，求圆C和直线PF的方程；
（2）若在点P处观测该圆形标志的最大视角（即
）的正切值为
,求该圆形标志物的半径．
已知直线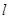
与圆
相交于A,B两点，弦AB的中点为
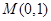
（1）求实数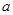
的取值范围以及直线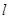的方程;
（2）若以AB为直径的圆过原点O，求圆C的方程．