.
已知各项均不为零的数列{an}的前n项和为Sn,且满足a 1=c,2Sn=anan+1+r.
1=c,2Sn=anan+1+r.
(1)若r=-6,数列{an}能否成为等差数列?若能,求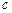 满足的条件;若不能,请说明理由.
满足的条件;若不能,请说明理由.
(2)设 ,
, ,
,
若r>c>4,求证:对于一切n∈N*,不等式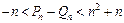 恒成立.
恒成立.
(本小题满分12分)如图, 为圆
为圆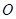 的直径,点
的直径,点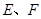 在圆
在圆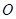 上,
上, ,矩形
,矩形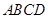 所在的平面和圆
所在的平面和圆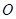 所在的平面互相垂直,且
所在的平面互相垂直,且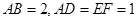 .
.
(1)求证: ;
;
(2)设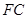 的中点为
的中点为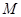 ,求证:
,求证: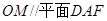 ;
;
(3)设平面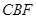 将几何体
将几何体 分成的两个椎体的体积分别为
分成的两个椎体的体积分别为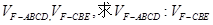 .
.
(本小题满分12分)已知函数 的图像的一部分如图所示.
的图像的一部分如图所示.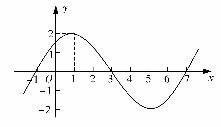
(1)求函数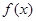 的解析式;
的解析式;
(2)求函数 的最小正周期和最值.
的最小正周期和最值.
(本小题满分14分)已知函数 的导函数。
的导函数。
(1)求证:曲线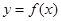 在点
在点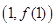 处的切线不过点
处的切线不过点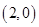 ;
;
(2)若在区间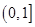 中存在
中存在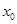 ,使得
,使得 ,求
,求 的取值范围;
的取值范围;
(3)若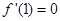 ,试证明:对任意
,试证明:对任意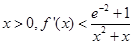 恒成立。
恒成立。
(本小题满分13分)
设数列 的前
的前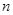 项和为
项和为 ,若对任意的正整数
,若对任意的正整数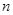 ,总存在正整数
,总存在正整数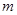 ,使得
,使得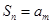 ,则称
,则称 是“
是“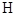 数列”。
数列”。
(1)若数列 的前
的前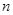 项和为
项和为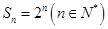 ,证明:
,证明: 是“
是“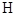 数列”;
数列”;
(2)设 是等差数列,其首项
是等差数列,其首项 ,公差
,公差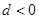 ,若
,若 是“
是“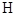 数列”,求
数列”,求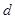 的值;
的值;
(3)证明:对任意的等差数列 ,总存在两个“
,总存在两个“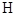 数列”
数列” ,使得
,使得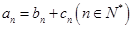 成立。
成立。
(本小题满分12分)已知函数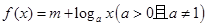 的图像过点
的图像过点 ,点
,点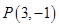 关于直线
关于直线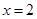 的对称点
的对称点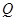 在
在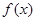 的图像上。
的图像上。
(1)求函数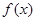 的解析式;
的解析式;
(2)令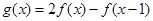 ,求
,求 的最小值及取得最小值时
的最小值及取得最小值时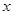 的值。
的值。