如图,两根足够长的平行金属导轨由倾斜和水平两部分平滑(图中未画出)连接组成,导轨间距L=1m,倾角θ=450,水平部分处于磁感强度B=1T的匀强磁场中磁场方向竖直向上,磁场左边界MN与导轨垂直。金属棒ab质量m1=0.2kg,电阻R1=1Ω,金属棒cd质量m2=0.2kg,电阻R2=3Ω,导轨电阻不计,两棒与导轨间动摩擦因数μ=0.2。开始时,棒ab放在斜导轨上,与水平导轨高度差h=1m,棒cd放在水平导轨上,距MN距离为S0。两棒均与导轨垂直,现将ab棒由静止释放,取g=10m/s2,求:⑴棒ab运动到MN处的速度大小;⑵棒cd运动的最大加速度;⑶若导轨水平部分光滑,要使两棒不相碰,棒cd距离MN的最小距离S0。
一辆质量为m=1000kg的汽车,从A点开始关闭发动机,之后只在阻力的作用下沿水平地面滑行了一段距离到达B点停止。已知汽车在A点的速度vA=12m/s;A点到B点的距离L=12m;求
(1)汽车在A点的动能EA=?
(2)从A到B这个过程中阻力做的功Wf=?
(3)从A到B这个过程中汽车受到的阻力的大小f=?
把一小球从距离水平地面高h=20m处,以v0=5m/s的初速度水平抛出,不计空气阻力, g=10m/s2。求:
(1)小球在空中飞行的时间t=?
(2)小球落地点离抛出点的水平位移x=?
如图所示,虚线 与 轴的夹角为 =60°,在此角范围内有垂直于 平面向外的匀强磁场,磁感应强度大小为 。一质量为 、电荷量为 ( >0)的粒子从左侧平行于 轴射入磁场,入射点为 。粒子在磁场中运动的轨道半径为 。粒子离开磁场后的运动轨迹与 轴交于 点(图中未画出),且 = 。不计重力。求 点到 点的距离和粒子在磁场中运动的时间。
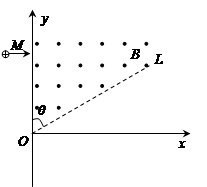
一电荷量为 ( >0)、质量为 的带电粒子在匀强电场的作用下,在 =0时由静止开始运动,场强随时间变化的规律如图所示。不计重力,求在 =0到 = 的时间间隔内

(1)粒子位移的大小和方向;
(2)粒子沿初始电场反方向运动的时间。
一客运列车匀速行驶,其车轮在轨道间的接缝处会产生周期性的撞击。坐在该客车中的某旅客测得从第1次到第16次撞击声之间的时间间隔为
。在相邻的平行车道上有一列货车,当该旅客经过货车车尾时,火车恰好从静止开始以恒定加速度沿客车行进方向运动。该旅客在此后的
内,看到恰好有30节货车车厢被他连续超过。已知每根轨道的长度为
,每节货车车厢的长度为
,货车车厢间距忽略不计。求
(1)客车运行的速度大小;
(2)货车运行加速度的大小。