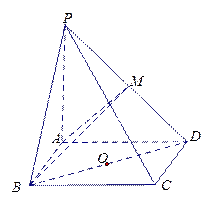
(理)(本小题8分)如图,在四棱锥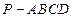 中,底面
中,底面 是矩形,
是矩形, 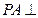 平面
平面 ,
,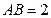 ,
, ,以
,以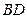 的中点
的中点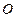 为球心
为球心 、
、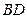 为直径的球面交
为直径的球面交 于点
于点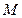 .
.
(1) 求证:平面
 平面
平面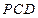 ;
;
(2)求点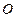 到平面
到平面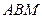 的距离.
的距离.
证明:(1)由题意,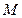 在以
在以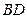 为直径
为直径 的球面上,则
的球面上,则
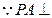 平面
平面 ,则
,则
又 ,
, 平面
平面 ,
,
∴ ,
,
 平面
平面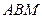 ,
,
∴平面 平面
平面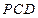 .
.
(2)∵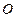 是
是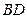 的中点,则
的中点,则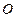 点到平面
点到平面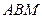 的距离等于点
的距离等于点 到平面
到平面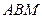 的距离的一半,由(1)知,
的距离的一半,由(1)知, 平面
平面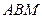 于
于 ,则线段
,则线段 的长就是点
的长就是点 到平面
到平面 的距离
的距离
∵在 中,
中,
∴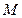 为
为 的中点,
的中点,
则点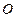 到平面
到平面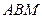 的距离为
的距离为
(其它方法可参照上述评分标准给分)
袋中有除颜色外完全相同的红、黄、白三种颜色的球各一个,从中每次任取1个.有放回地抽取3次,求: (1)3个全是红球的概率; (2)3个颜色全相同的概率;
(3)3个颜色不全相同的概率; (4)3个颜色全不相同的概率.
已知p:|1-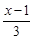 |≤2, q:x2-2x+1-m2≤0(m>0),若﹁p是﹁q的必要而不充分条件,求实数m的取值范围.
|≤2, q:x2-2x+1-m2≤0(m>0),若﹁p是﹁q的必要而不充分条件,求实数m的取值范围.
已知算法:(1)指出其功能(用算式表示),
 |
(2)将该算法用流程图描述.
(文)如图,|AB|=2,O为AB中点,直线 过B且垂直于AB,过A的动直线与
过B且垂直于AB,过A的动直线与 交于点C,点M在线段AC上,满足
交于点C,点M在线段AC上,满足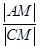 =
=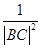 .
.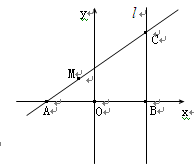
(I)求点M的轨迹方程;
(II)若过B点且斜率为- 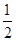 的直线与轨迹M交于点P,点Q(t,0)是x轴上任意一点,求当ΔBPQ为锐角三角形时t的取值范围.
的直线与轨迹M交于点P,点Q(t,0)是x轴上任意一点,求当ΔBPQ为锐角三角形时t的取值范围.
(理)已知数列{an}的前n项和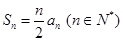 ,且
,且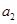 =1,
=1,
 .
.
(I)求数列{an}的通项公式;
(II)已知定理:“若函数f(x)在区间D上是凹函数,x>y(x,y∈D),且f’(x)存在,则有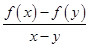
< f’(x)”.若且函数y=xn+1 在(0,+∞)上是凹函数,试判断bn与bn+1的大小;
在(0,+∞)上是凹函数,试判断bn与bn+1的大小;
(III)求证: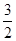 ≤bn<2.
≤bn<2.