探究函数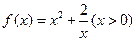
的最小值，并确定取得最小值时x的值. 列表如下, 请观察表中y值随x值变化的特点，完成以下的问题.
| x |
… |
0.25 |
0.5 |
0.75 |
1 |
1.1 |
1.2 |
1.5 |
2 |
3 |
5 |
… |
| y |
… |
8.063 |
4.25 |
3.229 |
3 |
3.028 |
3.081 |
3.583 |
5 |
9.667 |
25.4 |
… |
已知：函数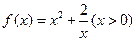在区间（0，1）上递减，问：
（1）函数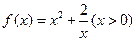在区间 上递增.当
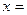时，
；
（2）函数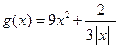
在定义域内有最大值或最小值吗？如有，是多少？此时x为何值？（直接回答结果，不需证明）
的最小值为
且关于
的不等式
的解集为
,
的零点个数．
，
．数列
的前
项和为
，且
．
，求数列
的前
．
中, 
+
又
和
的前
项和为
,求数列
的通项公式．
最大时,求
，满足
满足向量
，若
与
的数量积用含有
的代数式
表示．若
．
，求
与
的垂直，求实数
中， 
为其前
项和
，且
，求数列
的前
．