(文)(本小题8分)
如图,在四棱锥 中,
中, 平面
平面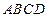 ,
,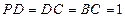 ,
,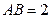 ,
, ,
,
(1)求证: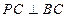 ;
;
(2)求点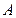 到平面
到平面 的距离
的距离
证明:(1) 平面
平面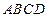 ,
, 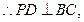 又
又
 平面
平面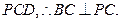
(2)设点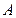 到平面
到平面 的距离为
的距离为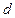 ,
, ,
, ,
,
求得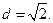 即点
即点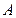 到平面
到平面 的距离为
的距离为
(其它方法可参照上述评分标准给分)
已知圆C: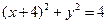 ,圆D的圆心D在y轴上,且与圆C外切,圆D与y轴交于A 、B两点,点
,圆D的圆心D在y轴上,且与圆C外切,圆D与y轴交于A 、B两点,点 P(-3,
P(-3, 0)
0)
(1)若点D的坐标为 (0,3),求
(0,3),求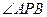 的正切值;
的正切值;
(2)当点D在y 轴上运动时,求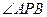 的最大值;
的最大值;
(3)在x轴上是否存在定点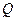 ,当圆D在y轴上运动时,
,当圆D在y轴上运动时,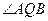 是定值?如果存在,求点
是定值?如果存在,求点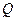 的坐标,如果不存在,说明理由.
的坐标,如果不存在,说明理由.
已知一元二次方程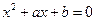 的一个根在-2与-1之间,另一个根在1与2之间,试求点
的一个根在-2与-1之间,另一个根在1与2之间,试求点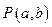 的轨迹及
的轨迹及 的范围.
的范围.
(本小题满分12分)
已知圆的方程是: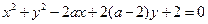 ,其中
,其中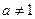 ,且
,且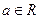 .
.
(1)求圆心的轨迹方程。
(2)求恒与圆相切的直线的方程;
( 本小题满分12分)
本小题满分12分)
求圆心在直线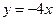 上,且与直线
上,且与直线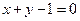 相切于
相切于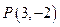
 的圆的方程.
的圆的方程.
(本小题满分10分)
已知直线过点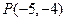 ,且与两坐标轴围成的三角形面积为5,求该直线方程。
,且与两坐标轴围成的三角形面积为5,求该直线方程。