定义:若数列 满足
满足 ,则称数列
,则称数列 为“平方递推数列”。已知数列
为“平方递推数列”。已知数列 中,
中, ,点
,点 在函数
在函数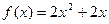 的图像上,其中
的图像上,其中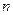 为正整数。
为正整数。
(Ⅰ)证明:数列 是“平方递推数列”,且数列
是“平方递推数列”,且数列 为等比数列。
为等比数列。
(Ⅱ)设(Ⅰ)中“平方递推数列”的前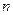 项之积为
项之积为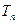 ,即
,即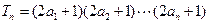 ,求数列
,求数列 的通项及
的通项及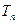 关于
关于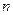 的表达式。
的表达式。
(Ⅲ)记 ,求数列
,求数列 的前
的前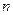 项之和
项之和 ,并求使
,并求使 的
的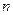 的最小值。
的最小值。
(本小题满分12分) 的三个内角
的三个内角 所对的边分别为
所对的边分别为 ,向量
,向量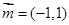 ,
, ,且
,且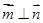 .
.
(1)求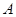 的大小;
的大小;
(2)现在给出下列三个条件:① ;②
;②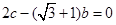 ;③
;③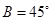 ,试从中再选择两个条件以确定
,试从中再选择两个条件以确定 ,求出所确定的
,求出所确定的 的面积.
的面积.
(本小题满分12分)已知函数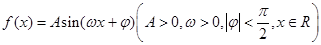 图象的一部分如图所示.
图象的一部分如图所示.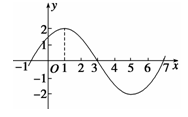
(1)求函数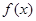 的解析式;
的解析式;
(2)当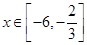 时,求函数
时,求函数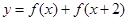 的最大值与最小值及相应的
的最大值与最小值及相应的 的值.
的值.
(本小题满分12分)已知点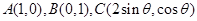
(1)若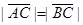 ,求
,求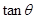 的值;
的值;
(2)若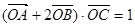 ,其中
,其中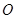 为坐标原点,求
为坐标原点,求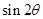 的值。
的值。
(本小题满分12分)已知函数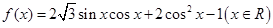 ).
).
(1)求函数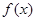 的最小正周期;
的最小正周期;
(2)若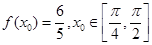 ,求
,求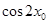 的值.
的值.
(本小题满分14分)设函数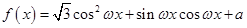 (其中
(其中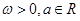 ),且
),且 的图象在
的图象在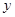 轴右侧的第一个最高点的横坐标为
轴右侧的第一个最高点的横坐标为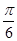 .
.
(1)求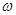 的值;
的值;
(2)如果 在区间
在区间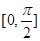 上有两个实数解,求
上有两个实数解,求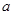 的取值范围.
的取值范围.