(
已知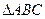 与
与 都是边长为2的等边三角形,且平面
都是边长为2的等边三角形,且平面 平面
平面 ,过点
,过点 作
作 平面
平面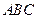 ,且
,且 .
.
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求直线 与平面
与平面 所成角的大小.
所成角的大小.
已知椭圆的中心在坐标原点,以坐标轴为对称轴,且经过两点P1( ,1)、P2(-
,1)、P2(- ,-
,-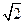 ),求椭圆方程.
),求椭圆方程.
若椭圆b2x2+a2y2=a2b2(a>b>0)的左焦点为F,右顶点为A,上顶点为B,且离心率为 ,求∠ABF.
,求∠ABF.
已知椭圆 =1(a>b>0)与x轴的正半轴交于点A,O是原点.若椭圆上存在一点M,使MA⊥MO,求椭圆离心率e的取值范围.
=1(a>b>0)与x轴的正半轴交于点A,O是原点.若椭圆上存在一点M,使MA⊥MO,求椭圆离心率e的取值范围.
如图,点A、B分别是椭圆 =1长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆上,且位于x轴上方,PA⊥PF.
=1长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆上,且位于x轴上方,PA⊥PF.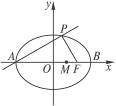
(1)求点P的坐标;
(2)设M是椭圆长轴AB上的一点,M到直线AP的距离等于|MB|,求椭圆上的点到点M的距离d的最小值.
设P为椭圆 =1(a>b>0)上任一点,F1、F2分别为左、右焦点,求|PF1|·|PF2|的最大、最小值.
=1(a>b>0)上任一点,F1、F2分别为左、右焦点,求|PF1|·|PF2|的最大、最小值.