我国西南地区正遭受着百年不遇的旱灾.据气象预报,未来48小时受灾最严重的甲地有望迎来一次弱降雨过程.某军区命令M 部队立即前往甲地准备实施人工增雨作业,已知“人工增雨”高炮车Ⅰ号载有3枚“增雨炮弹”和1枚“增雨火箭”,通过炮击“积雨云”实施增雨,第一次击中积雨云只能使云层中的水分子凝聚,第二次击中同一积雨云才能成功增雨.如果需要第4次射击才使用“增雨火箭”,当增雨成功或者增雨弹用完才停止射击.每次射击相互独立,且用“增雨炮弹
部队立即前往甲地准备实施人工增雨作业,已知“人工增雨”高炮车Ⅰ号载有3枚“增雨炮弹”和1枚“增雨火箭”,通过炮击“积雨云”实施增雨,第一次击中积雨云只能使云层中的水分子凝聚,第二次击中同一积雨云才能成功增雨.如果需要第4次射击才使用“增雨火箭”,当增雨成功或者增雨弹用完才停止射击.每次射击相互独立,且用“增雨炮弹 ”击中积雨云的概率是
”击中积雨云的概率是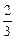 ,用“增雨火箭”击中积雨云的概率是
,用“增雨火箭”击中积雨云的概率是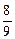 .
.


(Ⅰ) 求不使用“增雨火箭”就能成功增雨的概率;
求不使用“增雨火箭”就能成功增雨的概率;
(Ⅱ)求要使用“增雨火箭”才能成功增雨的概率;
(Ⅲ)求射击次数不小于3的概率.
(本小题满分12分)
已知向量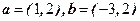 .
.
(1)求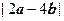 ;
;
(2)若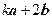 与
与 平行,求
平行,求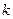 的值;
的值;
(3)若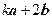 与
与 的夹角是钝角,求实数
的夹角是钝角,求实数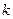 的取值范围.
的取值范围.
(本小题满分12分)
已知函数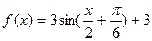 .
.
(1)用五点法画出它在一个周期内的闭区间上的图象;
(2)指出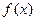 的周期、振幅、初相、对称轴;
的周期、振幅、初相、对称轴;
(3)写出函数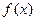 的单调递增区间.
的单调递增区间.
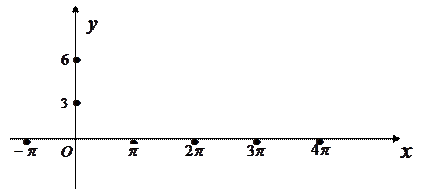
(本小题满分12分)
已知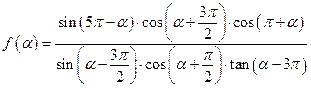 .
.
(1)化简 ;
;
(2)若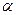 是第三象限角,且
是第三象限角,且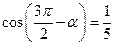 ,求
,求 的值.
的值.
(本小题满分14分)
已知函数 的减区间是
的减区间是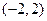 .
.
⑴试求 、
、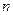 的值;
的值;
⑵求过点 且与曲线
且与曲线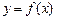 相切的切线方程;
相切的切线方程;
⑶过点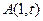 是否存在与曲线
是否存在与曲线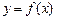 相切的3条切线,若存在,求实数t的取值范围;若不存在,请说明理由.
相切的3条切线,若存在,求实数t的取值范围;若不存在,请说明理由.
(本小题满分12分)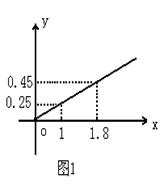

某民营企业生产A,B两种产品,根据市场调查和预测,A产品的利润与投资成正比,其关系如图1,B产品的利润与投资的算术平方根成正比,其关系如图2(注:利润与投资单位是万元).
⑴分别将A,B两种产品的利润表示为投资的函数,并写出它们的函数关系式;
⑵该企业已筹集到10万元资金,并全部投入A,B两种产品的生产,问:怎样分配这10万元投资,才能使企业获得最大利润.