(本小题满分12分)
已知函数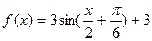 .
.
(1)用五点法画出它在一个周期内的闭区间上的图象;
(2)指出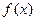 的周期、振幅、初相、对称轴;
的周期、振幅、初相、对称轴;
(3)写出函数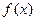 的单调递增区间.
的单调递增区间.
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
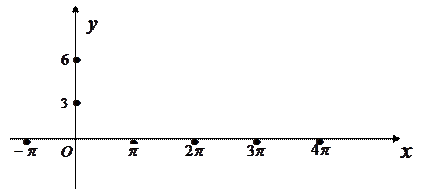
已知函数 .(Ⅰ)求不等式
.(Ⅰ)求不等式 的解集;
的解集;
(Ⅱ)若关于 的不等式
的不等式 的解集非空,求实数
的解集非空,求实数 的取值范围.
的取值范围.
如图,在正△ABC中,点D,E分别在边AC, AB上,且AD=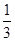 AC, AE=
AC, AE=  AB,BD,CE相交于点F。
AB,BD,CE相交于点F。
(I)求证:A,E,F,D四点共圆;
(Ⅱ)若正△ABC的边长为2,求,A,E,F,D所在圆的半径.
(本小题满分12分)设 和
和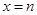 是函数
是函数 的两个极
的两个极
值点,其中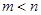 ,
, .(Ⅰ) 求
.(Ⅰ) 求 的取值范围;
的取值范围;
(Ⅱ) 若 ,求
,求 的最大值.
的最大值.
(本小题满分12分)如图,在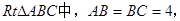 点
点 上,过点
上,过点 做
做 //
// 将
将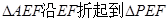 的位置(
的位置( ),
),
使得 .
.
(I)求证: (II)试问:当点
(II)试问:当点 上移动时,二面角
上移动时,二面角 的平面角的余弦值是否为定值?若是,求出定值,若不是,说明理由.
的平面角的余弦值是否为定值?若是,求出定值,若不是,说明理由.
(本小题满分12分)某校从6名学生会干部(其中男生4人,女生2人)中选3人参加市中学生运动会志愿者。(Ⅰ)所选3人中女生人数为ξ,求ξ的分布列及数学期望。
(Ⅱ)在男生甲被选中的情况下,求女生乙也被选中的概率