如图所示,在竖直平面内,粗糙的斜面轨道AB的下端与光滑的圆弧轨道BCD相切于B, C是最低点,圆心角∠BOC=37°,D与圆心O等高,圆弧轨道半径R=1.0m,现有一个质量为m=0.2kg可视为质点的小物体,从D点的正上方E点处自由下落,DE距离h=1.6m,物体与斜面AB之间的动摩擦因数μ=0.5。取sin37o=0.6,cos37o=0.8, g=10m/s2。求:
⑴物体第一次通过C点时轨道对物体的支持力FN的大小;
⑵要使物体不从斜面顶端飞出,斜面的长度LAB至少要多长;
⑶若斜面已经满足⑵要求,物体从E点开始下落,直至最后在光滑圆弧轨道做周期性运动,在此过程中系统因摩擦所产生的热量Q的大小。
如图所示,倾角为45°的光滑斜面AB与竖直的光滑半圆轨道在B点平滑连接,半圆轨道半径R=0.40m,一质量m=1.0kg的小物块在A点由静止沿斜面滑下,已知物块经过半圆轨道最高点C时对轨道的压力恰好等于零,物块离开半圆形轨道后落在斜面上的点为D(D点在图中没有标出)。g取10m/s2。求:A点距水平面的高度h。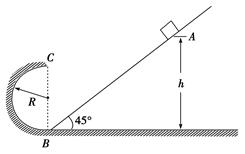
随着现代科学技术的飞速发展,广寒宫中的嫦娥不再寂寞,古老的月球即将留下中华儿女的足迹.航天飞机将作为能往返于地球与太空、可以重复使用的太空飞行器,备受人们的喜爱.宇航员现欲乘航天飞机对在距月球表面高h处的圆轨道上运行的月球卫星进行维修.试根据你所学的知识回答下列问题:
(1)维修卫星时航天飞机的速度应为多大?
(2)已知地球自转周期为T0,则该卫星每天可绕月球转几圈?(已知月球半径为R,月球表面的重力加速度为gm,计算过程中可不计地球引力的影响,计算结果用h、R、gm、T0等表示)
在光滑的水平面内,一质量m="1" kg的质点以速度v0="10" m/s沿x轴正方向运动,经过原点后受一沿y轴正方向上的水平恒力F="15" N作用,直线OA与x轴成α=37°,如下图所示曲线为质点的轨迹图(g取10 m/s2,sin 37°=0.6,cos 37°=0.8),求:如果质点的运动轨迹与直线OA相交于P点,质点从O点到P点所经历的时间以及P点的坐标; 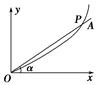
如图所示,光滑的 圆弧AB(质量可忽略)固定在甲车的左端,其半径R=1m。质量均为M="3" kg的甲、乙两辆小车静止于光滑水平面上,两车之间通过一感应开关相连(当滑块滑过感应开关时,两车自动分离)。其中甲车上表面光滑,乙车上表面与滑块P之间的动摩擦因数μ=0.4。将质量为m="2" kg的滑块P(可视为质点)从A处由静止释放,滑块P滑上乙车后最终未滑离乙车。求:
圆弧AB(质量可忽略)固定在甲车的左端,其半径R=1m。质量均为M="3" kg的甲、乙两辆小车静止于光滑水平面上,两车之间通过一感应开关相连(当滑块滑过感应开关时,两车自动分离)。其中甲车上表面光滑,乙车上表面与滑块P之间的动摩擦因数μ=0.4。将质量为m="2" kg的滑块P(可视为质点)从A处由静止释放,滑块P滑上乙车后最终未滑离乙车。求: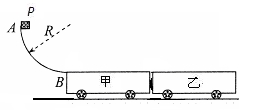
①滑块P刚滑上乙车时的速度大小;
②滑块P在乙车上滑行的距离为多大?
如图(a)所示,一导热性能良好、内壁光滑的气缸水平放置,横截面积为S=2×10-3m2、质量为m=4kg厚度不计的活塞与气缸底部之间封闭了一部分气体,此时活塞与气缸底部之间的距离为24cm,在活塞的右侧12cm处有一对与气缸固定连接的卡环,气体的温度为300K,大气压强P0=1.0×105Pa。现将气缸竖直放置,如图(b)所示,取g=10m/s2。求:
(1)活塞与气缸底部之间的距离;
(2)加热到675K时封闭气体的压强。