如图所示为某学校一套校内备用供电系统,由一台内阻为1Ω的发电机向全校22个教室( 每个教室有“220V,40W”的白炽灯6盏)供电。 白炽灯都正常发光。如果每条输电线的电阻R都是2Ω,升压变压器和降压变压器(都认为是理想变压器)的匝数比
每个教室有“220V,40W”的白炽灯6盏)供电。 白炽灯都正常发光。如果每条输电线的电阻R都是2Ω,升压变压器和降压变压器(都认为是理想变压器)的匝数比 分别是1:4和4:1,那么:
分别是1:4和4:1,那么: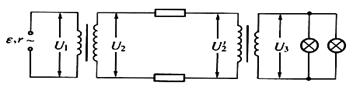
(1) 输电线上的电流是多大?
(2) 发电机的输出功率应是多大?
(3) 发电机的电动势是多大?
如图所示电路中,电源电动势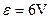 ,内阻
,内阻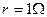 ,
,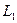 、
、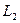 是两个相同的灯泡,均标有“4V,4W”字样.
是两个相同的灯泡,均标有“4V,4W”字样.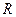 是滑线变阻器,标有“50Ω,2A”字样.试求:
是滑线变阻器,标有“50Ω,2A”字样.试求:
(1)电键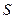 断开时,为使
断开时,为使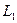 正常发光,变阻器
正常发光,变阻器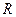 的阻值应调为多大?
的阻值应调为多大?
(2)电键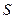 闭合时,为使
闭合时,为使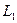 、
、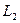 都正常发光,变阻器
都正常发光,变阻器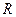 的阻值应调为多大?
的阻值应调为多大?
(3)以上两种情况中,电源输出的电功率各多大?
(4)具体分析说明,能否将规格相同的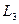 与
与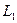 、
、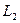 并联后,通过调节变阻器
并联后,通过调节变阻器 使三个灯泡都正常发光?
使三个灯泡都正常发光?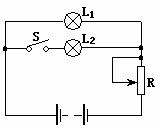
如图所示为两组平行板金属板,一组竖直放置,一组水平放置,今有一质量为m的电子静止在竖直放置的平行金属板的A点,经电压U0加速后通过B点进入两板间距为d、电压为U的水平放置的平行金属板间,若电子从两块水平平行板的正中间射入,且最后电子刚好能从右侧的两块平行金属板穿出,A、B分别为两块竖直板的中点,求:
(1)电子通过B点时的速度大小;
(2)右侧平行金属板的长度;
(3)电子穿出右侧平行金属板时的动能。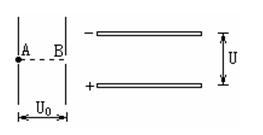
如图所示电路中,电源电动势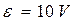 和内阻
和内阻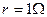 的相同电池串联组成,定值电阻
的相同电池串联组成,定值电阻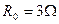 .为使可变电阻
.为使可变电阻 获得4W的电功率,应将
获得4W的电功率,应将 的阻值调为多大?
的阻值调为多大?
如图所示,在空间加水平向右的匀强电场,绝缘细线一端固定于O点,另一端连接一带电荷量为q,质量为m的带正电小球,要使带电小球静止时细线与竖直方向成а角,则所加的匀强电场多大?这时细线中的张力多大?
飞行时间质谱仪可对气体分子进行分析。如图所示,在真空状态下,脉冲阀P喷出微量气体,经激光照射产生电荷量为q、质量为m的正离子,自a板小孔进入a、b间的加速电场,从b板小孔射出,沿中线方向进入M、N板间的偏转控制区,到达探测器。已知a、b板间距为d,极板M、N的长度和间距均为L。不计离子重力及进入a板时的初速度。
(1)当a、b间的电压为U1,在M、N间加上适当的电压U2,使离子到达探测器。求离子从a板到达探测器的飞行时间。
(2)为保证离子不打在极板上,试求U2与U1的关系。
|