已知某射手射击一次,击中目标的概率是 .(1)求连续射击5次,恰有3次击中目标的概率;
.(1)求连续射击5次,恰有3次击中目标的概率;
(2)求连续射击5次,击中目标的次数X的数学期望和方差.
(3)假设连续2次未击中目标,则中止其射击,求恰好射击5次后,被中止射击的概率.(本题结果用分数表示即可).
(本小题满分12分)
已知关于x的二次函数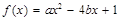 .
.
(I)设集合P={1,2,3}和Q={-1,1,2,3,4},分别从集合P和Q中随机取一个数作为a和b,求函数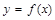 在区间
在区间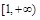 上是增函数的概率;
上是增函数的概率;
(II)设点(a,b)是区域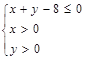 内的一点,求函数
内的一点,求函数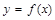 在区间
在区间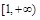 上是增函数的概率.
上是增函数的概率.
本小题满分12分)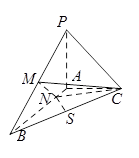
已知三棱锥PABC中,PA⊥平面ABC,AB⊥AC,PA=AC=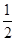 AB,
AB,
N为AB上一点,AB=4AN,M,S分别为PB,BC的中点.
(I)证明:CM⊥SN;(II)求SN与平面CMN所成角的大小.
(本小题满分12分)
已知函数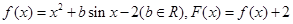 ,且对于任意实数
,且对于任意实数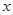 ,恒有
,恒有 .
.
(1)求函数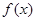 的解析式;
的解析式;
(2)函数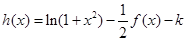 有几个零点?
有几个零点?
(本小题满分12分)
设函数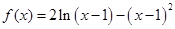 .
.
(1)求函数 的单调递增区间;
的单调递增区间;
(2)若关于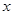 的方程
的方程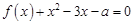 在区间
在区间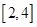 内恰有两个相异的实根,求实数
内恰有两个相异的实根,求实数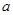 的取值范围.
的取值范围.
(本小题满分12分)
已知向量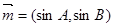 ,
, ,
,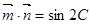 ,且
,且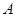 、
、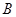 、
、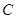 分别为
分别为 的三边
的三边 、
、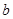 、
、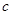 所对的角。
所对的角。
(1)求角C的大小;
(2)若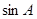 ,
, ,
,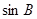 成等差数列,且
成等差数列,且 ,求
,求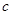 边的长。
边的长。