在等差数列{an}中,前n项的和为Sn.已知a7=10,a27=50.
(1)求a17;
(2)求a10+a11+a12+…+a30 .
(本题满分10分,每小题各5分)
(1)求值: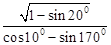
(2)求证: ,
,
(本小题满分14分)已知椭圆 (
( )经过点
)经过点 ,且椭圆的左、右焦点分别为
,且椭圆的左、右焦点分别为 、
、 ,过椭圆的右焦点
,过椭圆的右焦点 作两条互相垂直的直线,分别交椭圆于点
作两条互相垂直的直线,分别交椭圆于点 、
、 及
及 、
、 .
.
(1)求椭圆的方程;
(2)求 的值;
的值;
(3)求 的最小值.
的最小值.
(本小题满分14分)已知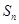 为数列
为数列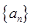 的前
的前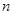 项和,且有
项和,且有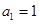 ,
,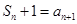 (
(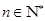 ).
).
(1)求数列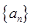 的通项公式;
的通项公式;
(2)若数列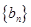 满足
满足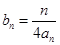 ,其前
,其前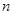 项和为
项和为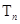 ,求证:
,求证: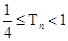 .
.
(本小题满分14分)如图,在四棱柱 中,底面
中,底面 是等腰梯形,
是等腰梯形, ,
, ,
, 是线段
是线段 的中点.
的中点.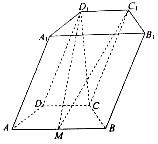
(1)求证: 平面
平面 ;
;
(2)若 平面
平面 且
且 ,求平面
,求平面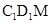 和平面
和平面 所成的角(锐角)的余弦值.
所成的角(锐角)的余弦值.
(本小题满分14分)某农场计划种植甲、乙两个品种的蔬菜,总面积不超过 亩,总成本不超过
亩,总成本不超过 万元.甲、乙两种蔬菜的成本分别是每亩
万元.甲、乙两种蔬菜的成本分别是每亩 元和每亩
元和每亩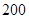 元.假设种植这两个品种的蔬菜,能为该农场带来的收益分别为每亩
元.假设种植这两个品种的蔬菜,能为该农场带来的收益分别为每亩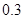 万元和每亩
万元和每亩 万元.问该农场如何分配甲、乙两种蔬菜的种植面积,可使农场的总收益最大,最大收益是多少万元?
万元.问该农场如何分配甲、乙两种蔬菜的种植面积,可使农场的总收益最大,最大收益是多少万元?