(本小题满分14分)如图,在四棱柱 中,底面
中,底面 是等腰梯形,
是等腰梯形, ,
, ,
, 是线段
是线段 的中点.
的中点.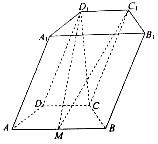
(1)求证: 平面
平面 ;
;
(2)若 平面
平面 且
且 ,求平面
,求平面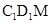 和平面
和平面 所成的角(锐角)的余弦值.
所成的角(锐角)的余弦值.
(本小题满分12分)函数 的一系列对应值如下表:
的一系列对应值如下表:
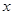 |
…… |
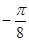 |
0 |
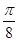 |
 |
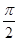 |
 |
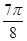 |
…. |
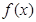 |
….. |
0 |
1 |
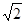 |
0 |
—1 |
 |
0 |
….. |
(1)根据表中数据求出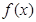 的解析式;
的解析式;
(2)指出函数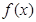 的图象是由函数
的图象是由函数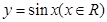 的图象经过怎样的变化而得到的;
的图象经过怎样的变化而得到的;
(3)令 ,若
,若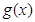 在
在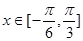 时有两个零点,求
时有两个零点,求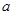 的取值范围。
的取值范围。
(本小题满分12分)已知a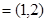 ,b
,b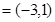 .
.
(1) 求a -2b;
(2) 设a, b的夹角为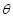
 ,求
,求 的值;
的值;
(3)若向量a+kb与a-kb互相垂直,求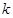 的值.
的值.
(本小题满分12分)已知函数 ;
;
(1)若 ,求
,求 的值域;
的值域;
(2)在(1)的条件下,判断 的单调性;
的单调性;
(3)当 时
时 有意义求实
有意义求实 的范围。
的范围。
(本小题满分10分)已知函数 ;
;
(1)若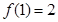 ,求
,求 的值,并作出
的值,并作出 的图象;
的图象;
(2)当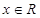 时,恒有
时,恒有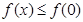 求
求 的取值范围。
的取值范围。
已知函数 .
.
(1)求 的单调区间;
的单调区间;
(2)求 在区间
在区间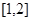 上的最小值;
上的最小值;
(3)设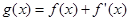 ,当
,当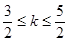 时,对任意
时,对任意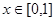 ,都有
,都有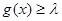 成立,求实数
成立,求实数 的取值范围。
的取值范围。