设 ,在线段
,在线段 上任取两点C,D(端点
上任取两点C,D(端点 除外),将线段
除外),将线段 分成三条线段AC,CD,DB.
分成三条线段AC,CD,DB.
(1)若分成的三条线段的长度均为正整数,求这三条线段可以构成三角形(称事件A)的概率;
(2)若分成的三条线段的长度均为正实数,求这三条线段可以构成三角形(称事件B)的概率;
(3)根据以下用计算机所产生的20组随机数,试用随机数摸拟的方法,来近似计算(Ⅱ)中事件B的概率.
20组随机数如下:
| |
1组 |
2组 |
3组 |
4组 |
5组 |
6组 |
7组 |
8组 |
9组 |
10组 |
| X |
0.52 |
0.36 |
0.58 |
0.73 |
0.41 |
0. 6 6 |
0.05 |
0.32 |
0.38 |
0.73 |
| Y |
0.76 |
0.39 |
0.37 |
0.01 |
0.04 |
0.28 |
0.03 |
0.15 |
0.14 |
0 .86 .86 |
| |
11组 |
12组 |
13组 |
14组 |
15组 |
16组 |
17组 |
18组 |
19组 |
20组 |
| X |
0.67 |
0.47 |
0.58 |
0.21 |
0.54 |
0. 64 64 |
0.36 |
0.35 |
0.95 |
0.14 |
| Y |
0.41 |
0.54 |
0.51 |
0.37 |
0.31 |
0.23 |
0.56 |
0.89 |
0.17 |
0.03 |
(X是 之间的均匀随机数,Y也是
之间的均匀随机数,Y也是 之间的均匀随机
之间的均匀随机 数)
数)
在 中,
中, 分别为角
分别为角 的对边,
的对边, 的面积S满足
的面积S满足
(Ⅰ)求角A的值;
(Ⅱ)若 ,设角B的大小为x,用x表示c,并求c的取值范围.
,设角B的大小为x,用x表示c,并求c的取值范围.
已知函数f(x)=|x-2|,g(x)=-|x+3|+m.
(1)解关于x的不等式f(x)+a-1>0(a∈R);
(2)若函数f(x)的图象恒在函数g(x)图象的上方,求m的取值范围.
已知直线l经过点 ,倾斜角α=
,倾斜角α= ,圆C的极坐标方程为
,圆C的极坐标方程为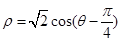 .
.
(1)写出直线l的参数方程,并把圆C的方程化为直角坐标方程;
(2)设l与圆C相交于两点A、B,求点P到A、B两点的距离之积.
如图,A、B是两圆的交点,AC是小圆的直径,D和E分别是CA和CB的延长线与大圆的交点,已知AC=4,BE=10,且BC=AD,求DE的长.
已知线段MN的两个端点M、N分别在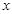 轴、
轴、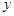 轴上滑动,且
轴上滑动,且 ,点P在线段MN上,满足
,点P在线段MN上,满足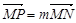
 ,记点P的轨迹为曲线W.
,记点P的轨迹为曲线W.
(1)求曲线W的方程,并讨论W的形状与 的值的关系;
的值的关系;
(2)当 时,设A、B是曲线W与
时,设A、B是曲线W与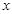 轴、
轴、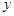 轴的正半轴的交点,过原点的直线与曲线W交于C、D两点,其中C在第一象限,求四边形ACBD面积的最大值.
轴的正半轴的交点,过原点的直线与曲线W交于C、D两点,其中C在第一象限,求四边形ACBD面积的最大值.