已知线段MN的两个端点M、N分别在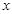 轴、
轴、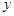 轴上滑动,且
轴上滑动,且 ,点P在线段MN上,满足
,点P在线段MN上,满足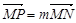
 ,记点P的轨迹为曲线W.
,记点P的轨迹为曲线W.
(1)求曲线W的方程,并讨论W的形状与 的值的关系;
的值的关系;
(2)当 时,设A、B是曲线W与
时,设A、B是曲线W与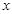 轴、
轴、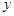 轴的正半轴的交点,过原点的直线与曲线W交于C、D两点,其中C在第一象限,求四边形ACBD面积的最大值.
轴的正半轴的交点,过原点的直线与曲线W交于C、D两点,其中C在第一象限,求四边形ACBD面积的最大值.
(本题共12分)
据统计某种汽车的最高车速为120千米∕时,在匀速行驶时每小时的耗油量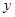 (升)与
(升)与
行驶速度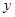 (千米∕时)之间有如下函数关系:
(千米∕时)之间有如下函数关系: 。已知甲、乙
。已知甲、乙
两地相距100千米。
(I)若汽车以40千米∕时的速度匀速行驶,则从甲地到乙地需耗油多少升?
(II)当汽车以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少为多少升?
(本题共10分)
将两块三角板按图甲方式拼好,其中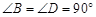 ,
,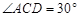 ,
,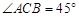 ,
,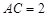 ,现将三角板
,现将三角板 沿
沿 折起,使
折起,使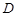 在平面
在平面 上的射影恰好在
上的射影恰好在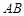 上,如图乙.
上,如图乙.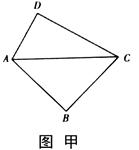
(Ⅰ)求证: 平面
平面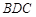 ;
;
(Ⅱ)求二面角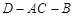 的余弦值;
的余弦值;
(本题共10分)
已知函数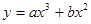 ,当
,当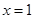 时,有极大值
时,有极大值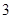 。
。
(Ⅰ)求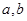 的值;
的值;
(Ⅱ)求函数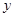 的极小值。
的极小值。
(本题共10分)
已知函数 。
。
(Ⅰ)若曲线 在
在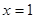 处的切线与直线
处的切线与直线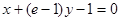 垂直,求
垂直,求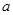 的值;
的值;
(Ⅱ)若函数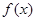 在区间(
在区间( ,
,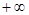 )内是增函数,求
)内是增函数,求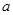 的取值范围。
的取值范围。
已知函数f(x)=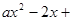 1 .
1 .
(1)试讨论函数f(x)的单调性;
(2)若  ,且f(x)在区间[1,3]上的最大值为M(a) ,最小值为N(a),
,且f(x)在区间[1,3]上的最大值为M(a) ,最小值为N(a),
令g(a)= M(a)-N(a),求 g(a)的表达式,试求g(a)的最小值.