已知函数 ,在定义域内有且只有一个零点,存在
,在定义域内有且只有一个零点,存在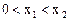 , 使得不等式
, 使得不等式 成立. 若
成立. 若 ,
, 是数列
是数列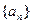 的前
的前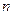 项和.
项和.
(I)求数列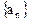 的通项公式;
的通项公式;
(II)设各项均不为零的数列 中,所有满足
中,所有满足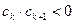 的正整数
的正整数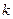 的个数称为这个数列
的个数称为这个数列 的变号数,令
的变号数,令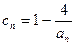 (n为正整数),求数列
(n为正整数),求数列 的变号数;
的变号数;
(Ⅲ)设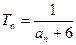 (
(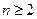 且
且 ),使不等式
),使不等式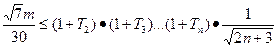 恒成立,求正整数
恒成立,求正整数 的最大值
的最大值
直线l在两坐标轴上的截距相等,且P(4,3)到直线l的距离为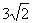 ,求直线l的方程.
,求直线l的方程.
试求三条直线ax+y+1=0,x+ay+1=0,x+y+a=0构成三角形的条件.
已知a为实数,求当直线l1:ax+y+1=0与l2:x+y-a=0相交时的交点坐标.
某商品的市场需求量y1(万件)、市场供应量y2(万件)与市场价格x(元/件)分别近似地满足下列关系:y1=-x+70,y2=2x-20.当y1=y2时的市场价格称为市场平衡价格,此时的需求量称为平衡需求量.
(1)求平衡价格和平衡需求量;
(2)若要使平衡需求量增加4万件,政府对每件商品应给予多少元补贴?
已知数列{ a n}的各项都是正数,且满足:a0=1,an+1= an·(4-an)(n∈N).
an·(4-an)(n∈N).
证明:an<an+1<2(n∈N).