(本小题共13分)
用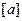 表示不大于
表示不大于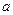 的最大整数.令集合
的最大整数.令集合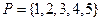 ,对任意
,对任意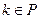 和
和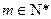 ,定义
,定义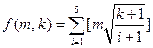 ,集合
,集合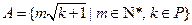 ,并将集合
,并将集合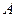 中的元素按照从小到大的顺序排列,记为数列
中的元素按照从小到大的顺序排列,记为数列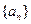 .
.
(Ⅰ)求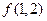 的值;
的值;
(Ⅱ)求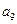 的值;
的值;
(Ⅲ)求证:在数列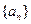 中,不大于
中,不大于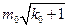 的项共有
的项共有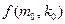 项.
项.
若对于一切实数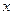 、
、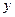 ,都有
,都有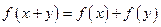
(1)求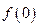 并证明
并证明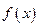 为奇函数;
为奇函数;
(2)若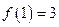 ,求
,求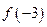 。
。
( 本小题满分16分)
本小题满分16分)
设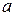 为实数,函数
为实数,函数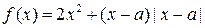 .
.
(1)若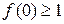 ,求
,求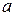
 的
的 取值范围;
取值范围;
(2)求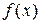 的最小值;
的最小值;
(3)设函数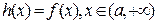 ,直接写出(不需给出演算步骤)不等式
,直接写出(不需给出演算步骤)不等式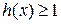 的解集.
的解集.
(本小题满分12分)
如图,三定点A(2,1),B(0,-1),C(-2,1); 三 动点D,E,M满足="t," =" t" ,
="t" , t∈[0,1].
(Ⅰ) 求动直线DE斜率的变化范围;
(Ⅱ) 求动点M的轨迹方程.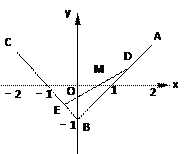
(本小题满分12分)
已知数列 中,
中, 是其前
是其前 项和,并且
项和,并且 ,
,
⑴设数列 ,求证:数列
,求证:数列 是等比数列;
是等比数列;
⑵设数列 ,求证:数列
,求证:数列 是等差数列;
是等差数列;
⑶求数列 的通项公式及前
的通项公式及前 项和。
项和。
(本小题满分10分)
某单位建造一间地面面积为12m2的背面靠墙的矩形小房,由于地理位置的限制,房子侧面的长度x不得超过 米,房屋正面的造价为400元/m2,房屋侧面
米,房屋正面的造价为400元/m2,房屋侧面 的造价为150元
的造价为150元 /m2,屋顶和地面的造价费用合计为5800元,如果墙高为3m,且不计房屋背面的费用.
/m2,屋顶和地面的造价费用合计为5800元,如果墙高为3m,且不计房屋背面的费用.
(1)把房屋总造价 表示成
表示成 的函数,并写出该函数的定义域.
的函数,并写出该函数的定义域.
(2)当侧面的长度为多少时,总造价最底?最低总造价是多少?