(本小题满分12分)如图,在多面体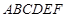 中,底面
中,底面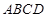 是边长为
是边长为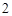 的的菱形,
的的菱形,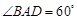 ,四边形
,四边形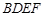 是矩形,平面
是矩形,平面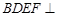 平面
平面 ,
,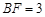 ,
, 和
和 分别是
分别是 和
和 的中点.
的中点.
(Ⅰ)求证:平面 平面
平面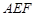 ;
;
(Ⅱ)求二面角 的大小.
的大小.
如图,一矩形铁皮的长为8cm,宽为5cm,在四个角上
截去四个相同的小正方形,制成一个无盖的小盒子.
(1)将小盒子的容积V写成关于小正方形的边长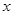 的函数;
的函数;
(2)正方形的边长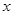 为多少时,盒子容积最大?求出最大值.
为多少时,盒子容积最大?求出最大值.
命题 :方程
:方程 有两个不等的正实数根,命题
有两个不等的正实数根,命题 :函数
:函数 在R上是减函数.若“
在R上是减函数.若“ 或
或 ”为真命题,“
”为真命题,“ 且
且 ” 为假命题,求
” 为假命题,求 的取值范围.
的取值范围.
一个容量为M的样本数据,其频率分布表如下.
(Ⅰ)完成频率分布表 ;
(Ⅱ)画出频率分布直方图 ;
(Ⅲ)利用频率分布直方图,估计总体的众数、中位数及平均数. 【解】 频率分布表频率分布直方图
【解】 频率分布表频率分布直方图
| 分组 |
频数 |
频率 |
| (10,20] |
2 |
0.10 |
| (20,30] |
3 |
|
| (30,40] |
4 |
0.20 |
| (40,50] |
||
| (50,60] |
4 |
0.20 |
| (60,70] |
2 |
0.10 |
| 合计 |
1.00 |
已知函数
(1)当 =
= 时,求曲线
时,求曲线 在点(
在点( ,
, )处的切线方程。
)处的切线方程。
(2)若函数 在(1,
在(1, )上是减函数,求实数
)上是减函数,求实数 的取值范围;
的取值范围;
(3)是否存在实数 若不存在,说明理由。若存在,求出
若不存在,说明理由。若存在,求出 的值,并加以证明。
的值,并加以证明。
已知椭圆的中心是坐标原点 ,焦点在
,焦点在 轴上,离心率为
轴上,离心率为 ,又椭圆上任一点到两焦点的距离和为
,又椭圆上任一点到两焦点的距离和为 .过右焦点
.过右焦点 与
与 轴不垂直的直线
轴不垂直的直线 交椭圆于
交椭圆于 ,
, 两点。
两点。
(1)求椭圆的方程;
(2)在线段 上是否存在点
上是否存在点 ,使得
,使得 ?若存在,求出
?若存在,求出 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.