已知非零实数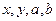 ,
,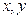 分别为
分别为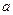 与
与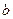 ,
,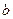 与
与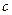 的等差中项,`且满足
的等差中项,`且满足 ,求证:非零实数
,求证:非零实数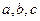 成等比数列.
成等比数列.
在圆心角为90°的扇形AOB中,以圆心O为起点作射线OC,求使得∠AOC和∠BOC都不小于30°的概率.
在Rt△ABC中,∠A=30°,过直角顶点C作射线CM交线段AB于M,求使|AM|>|AC|的概率.
有一段长为10米的木棍,现要截成两段,每段不小于3米的概率有多大?
袋中装有黑球和白球共7个,从中任取两个球都是白球的概率为 .现有甲、乙两人从袋中轮流摸球,甲先取,乙后取,然后甲再取……取后不放回,直到两人中有1人取到白球时即终止.每个球在每一次被取出的机会是等可能的.
.现有甲、乙两人从袋中轮流摸球,甲先取,乙后取,然后甲再取……取后不放回,直到两人中有1人取到白球时即终止.每个球在每一次被取出的机会是等可能的.
(1)求袋中原有白球的个数;
(2)求取球2次终止的概率;
(3)求甲取到白球的概率.
箱中有a个正品,b个次品,从箱中随机连续抽取3次,在以下两种抽样方式下:(1)每次抽样后不放回;(2)每次抽样后放回.求取出的3个全是正品的概率.