某工厂对某产品的产量与单位成本的资料分析后有如下数据:
| 月 份 |
1 |
2 |
3 |
4 |
5 |
6 |
| 产量x千件 |
2 |
3 |
4 |
3 |
4 |
5 |
| 单位成本y元/件 |
73 |
72 |
71 |
73 |
69 |
68 |
(Ⅰ) 画出散点图,并判断产量与单位成本是否线性相关。
(Ⅱ) 求单位成本y与月产量x之间的线性回归方程。(其中已计算得: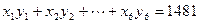 ,结果保留两位小数)
,结果保留两位小数)
某电视生产企业有A、B两种型号的电视机参加家电下乡活动,若企业投放A、B两种型号电视机的价值分别为a、b万元,则农民购买电视机获得的补贴分别为 万元(m>0且为常数).已知该企业投放总价值为10万元的A、B两种型号的电视机,且A、B两种型号的投放金额都不低于1万元.
万元(m>0且为常数).已知该企业投放总价值为10万元的A、B两种型号的电视机,且A、B两种型号的投放金额都不低于1万元.
(1)请你选择自变量,将这次活动中农民得到的总补贴表示为它的函数,并求其定义域;
(2)求当投放B型电视机的金额为多少万元时,农民得到的总补贴最大?
如图,在等腰梯形ABCD中,AB∥DC,AB = 4,CD = 2,等腰梯形的高为3,O为AB中点,PO⊥平面ABCD,垂足为O,PO = 2,EA∥PO.
(1)求证:BD⊥平面EAC;
(2)求二面角E—AC—P的平面角的余弦值.
“上海世博会”将于2010年5月1日至10月31日在上海举行。世博会“中国馆·贵宾厅”作为接待中外贵宾的重要场所,其中陈列的艺术品是体现兼容并蓄、海纳百川的重要文化载体,为此,上海世博会事物协调局将举办“中国2010年上海世博会‘中国馆·贵宾厅’艺术品方案征集”活动.某地美术馆从馆藏的中国画、书法、油画、陶艺作品中各选一件代表作参与应征,假设这四件代表作中中国画、书法、油画入选“中国馆·贵宾厅”的概率均为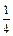 ,陶艺入选“中国馆·贵宾厅”的概率为
,陶艺入选“中国馆·贵宾厅”的概率为 .假定这四件作品是否入选相互没有影响.
.假定这四件作品是否入选相互没有影响.
(1)求该地美术馆选送的四件代表作中恰有一件作品入选“中国馆·贵宾厅”的概率;
(2)设该地美术馆选送的四件代表作中入选“中国馆·贵宾厅”的作品件数为随机变量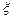 ,求
,求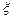 的数学期望.
的数学期望.
已知向量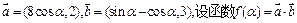 .
.
(1)求函数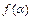 的最大值;
的最大值;
(2)在锐角三角形ABC中,角A、B、C的对边分别为a、b、c, 且△ABC的面积为3,
且△ABC的面积为3, a的值.
a的值.
己知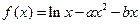 .
.
(Ⅰ)若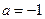 ,函数
,函数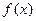 在其定义域内是增函数,求
在其定义域内是增函数,求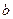 的取值范围;
的取值范围;
(Ⅱ)当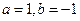 时,证明函数
时,证明函数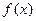 只有一个零点;
只有一个零点;
(Ⅲ)若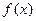 的图象与
的图象与 轴交于
轴交于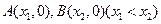 两点,
两点, 中点为
中点为 ,求证:
,求证: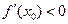 .
.