某牛奶加工厂现有鲜奶10吨,若在市场上直接销售,每吨可获取利润500元,制成酸奶销售,每吨可获利润1200元,制成奶片销售,每吨可获利润2000元,该工厂的生产能力为:如制成酸奶,每天可加工3吨,制成奶片每天可加工1吨,受人员限制,两种加工方式不能同时进行,受气温条件限制,这批牛奶必须在4天内全部销售或加工完毕,为此,该加工厂设计了两种可行性方案:
方案一:尽可能多的制成奶片,其余直接销售鲜牛奶。
方案二:将一部分制成奶片,其余制成酸奶销售,并恰好4天完成。
你认为选择哪种方案获利最多,为什么。(本题12分)
如图,小明在M处用高1米(DM=1米)的测角仪测得旗杆AB的顶端B的仰角为30°,再向旗杆方向前进10米到F处,又测得旗杆顶端B的仰角为60°,请求出旗杆AB的高度(取 ≈1.73,结果保留整数)
≈1.73,结果保留整数)
为了解本校九年级学生期末数学考试情况,销量在九年级随机抽取了一部分学生的期末数学成绩为样本,分为A、B(89~80分)、C(79~60分)、D(59~0分)四个等级进行统计,并将统计结果绘制成如下统计图,请你根据统计图解答以下问题:
(1)这次随机抽取的学生共有多少人?
(2)请补全条形统计图;
(3)这个学校九年级共有学生1200人,若分数为80分(含80分)以上为优秀,请估计这次九年级学生期末数学考试成绩为优秀的学生人数大约有多少?
将油箱注满k升油后,轿车科行驶的总路程S(单位:千米)与平均耗油量a(单位:升/千米)之间是反比例函数关系S=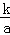 (k是常数,k≠0).已知某轿车油箱注满油后,以平均耗油量为每千米耗油0.1升的速度行驶,可行驶700千米.
(k是常数,k≠0).已知某轿车油箱注满油后,以平均耗油量为每千米耗油0.1升的速度行驶,可行驶700千米.
(1)求该轿车可行驶的总路程S与平均耗油量a之间的函数解析式(关系式);
(2)当平均耗油量为0.08升/千米时,该轿车可以行驶多少千米?
化简求值: •(
•( ),其中x=
),其中x= .
.
如图,AC是⊙O的直径,PA切⊙O于点A,点B是⊙O上的一点,且∠BAC=30°,∠APB=60°.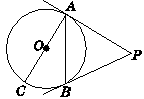
(1)求证:PB是⊙O的切线;
(2)若⊙O的半径为2,求弦AB及PA,PB的长.