将油箱注满k升油后，轿车科行驶的总路程S（单位：千米）与平均耗油量a（单位：升/千米）之间是反比例函数关系S=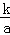
（k是常数，k≠0）．已知某轿车油箱注满油后，以平均耗油量为每千米耗油0.1升的速度行驶，可行驶700千米．
（1）求该轿车可行驶的总路程S与平均耗油量a之间的函数解析式（关系式）；
（2）当平均耗油量为0.08升/千米时，该轿车可以行驶多少千米？
市某楼盘准备以每平方米6 000元的均价对外销售，由于国务院有关房地产的新政策出台后，购房者持币观望，房地产开发商为了加快资金周转，对价格经过两次下调后，决定以每平方米4 860元的均价开盘销售.
（1）求平均每次下调的百分率.
（2）某人准备以开盘价均价购买一套100平方米的住房，开发商给予以下两种优惠方案以供选择：①打9.8折销售；②不打折，一次性送装修费每平方米80元，试问哪种方案更优惠？
已知等腰三角形的一个内角是
，求另外两个角的度数。
已知等腰三角形的一个内角是
，求另外两个角的度数；
已知|a|="5,|b|=2,ab" <0．求：3a +2b 的值．
解：∵|a|=5,∴a =_______．
∵|b|=2,∴b =_______．
∵ab <0,∴当a =_______时，b =_______,
当a =_______时，b＝_______．
∴3a +2b =_______或3a +2b =_______．
∴3a +2b 的值为_______．
小吃店一周中每天的盈亏情况如下（盈余为正）：128．3元，－25．6元，－15元，27元，－7元，36．5元，98元，一周总的盈亏情况如何？