掷两枚硬币,规定落地后,国徽朝上为正,国徽朝下为“反”,则会出现以下三种情况.

“正正” “反反”
“正反”
分别求出每种情况的概率.
(1)小刚做法:通过列表可知,每种情况都出现一次,因此各种情况发生的概率均占 .
.
| 可能出现的情况 |
正正 |
正反 |
反反 |
| 概率 |
 |
 |
 |

小敏的做法:
| 第一枚硬币的可能情况 第二枚硬币的可能情况 |
正 |
反 |
| 正 |
正正 |
反正 |
| 反 |
正反 |
反反 |
通过以上列表,小敏得出:“正正”的情况发生概率为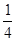 .“正反”的情况发生的概率为
.“正反”的情况发生的概率为 ,“反反”的情况发生的概率为
,“反反”的情况发生的概率为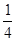 .
.
(1)以上三种做法,你同意哪种,说明你的理由;
(2)用列表法求概率时要注意哪些?
如图,在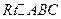 中,
中,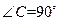 ,
,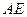 平分
平分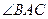 交
交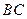 于
于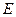 ,点
,点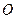 在
在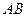 上,以
上,以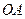 为半径的圆,交
为半径的圆,交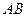 于
于 ,交
,交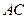 于
于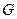 ,且点
,且点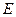 在⊙
在⊙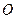 上,连结
上,连结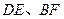 ,切⊙
,切⊙ 于点
于点 。
。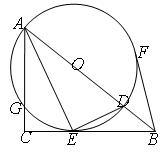
(1)求证
 ;
;(2)若
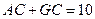 ,求⊙
,求⊙ 的半径;
的半径;
已知一元二次方程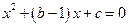
(1)若
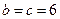 ,求该方程的根;
,求该方程的根;(2)若
 ,判断该方程的根的情况;
,判断该方程的根的情况;(3)若
 是该方程的两个根,且
是该方程的两个根,且 ,求证
,求证 。
。
如图, 内接于⊙
内接于⊙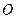 ,点
,点 在
在 的延长线上,
的延长线上,

(1)求证直线
 是⊙
是⊙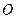 的切线;
的切线;(2)若
 ,求
,求 的长。
的长。
如图,有一块矩形铁皮,长 ,宽
,宽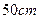 ,在他的四角各切去一个同样的正方形,然后将四周突出部分折起,就能制作一个无盖方盒。如果要制作的无盖方盒的底面积为
,在他的四角各切去一个同样的正方形,然后将四周突出部分折起,就能制作一个无盖方盒。如果要制作的无盖方盒的底面积为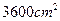 ,那么铁皮各角应切去边长为多大的正方形?
,那么铁皮各角应切去边长为多大的正方形?
已知在正方形网格上建立的平面直角坐标系中, 的位置如图所示
的位置如图所示(1)将
 绕点
绕点 顺时针方向旋转
顺时针方向旋转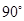 后得
后得
①直接写出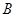 点的对应点
点的对应点 的坐标;
的坐标;
②求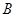 点旋转到点
点旋转到点 所经过的路线长(结果保留
所经过的路线长(结果保留 )
)(2)在正方形网格中,每个小正方形的顶点称为格点,在图中确定格点
 ,并画出以
,并画出以 为顶点的四边形,使其为中心对称图形(画一个即可)。
为顶点的四边形,使其为中心对称图形(画一个即可)。