已知函数f(x)=aln x-ax-3(a∈R).
(1)若a=-1,求函数f(x)的单调区间;
(2)若函数y=f(x)的图象在点(2,f(2))处的切线的倾斜角为45°,对于任意的t∈[1,2],函数g(x)=x3+x2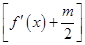 (f′(x)是f(x)的导数)在区间(t,3)上总不是单调函数,求m的取值范围;
(f′(x)是f(x)的导数)在区间(t,3)上总不是单调函数,求m的取值范围;
(3)求证: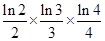 ×…×
×…× <
< (n≥2,n∈N*).
(n≥2,n∈N*).
已知抛物线C:y2=2px(p>0)过点A(1,-2).
(1)求抛物线C的方程,并求其准线方程;
(2)是否存在平行于OA(O为坐标原点)的直线l,使得直线l与抛物线C有公共点,且直线OA与l的距离等于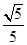 ?若存在,求出直线l的方程;若不存在,说明理由.
?若存在,求出直线l的方程;若不存在,说明理由.
如图,在四棱锥A—BCC1B1中,等边三角形ABC所在平面与正方形BCC1B1所在平面互相垂直,D为CC1的中点.
(1)求证:BD⊥AB1;
(2)求二面角B—AD—B1的余弦值.
已知数列{an}中,a1=2,an=2- (n≥2,n∈N*).
(n≥2,n∈N*).
(1)设bn= ,n∈N*,求证:数列{bn}是等差数列;
,n∈N*,求证:数列{bn}是等差数列;
(2)设cn= (n∈N*),求数列{cn}的前n项和Sn.
(n∈N*),求数列{cn}的前n项和Sn.
假设某班级教室共有4扇窗户,在每天上午第三节课上课预备铃声响起时,每扇窗户或被敞开或被关闭,且概率均为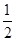 ,记此时教室里敞开的窗户个数为X.
,记此时教室里敞开的窗户个数为X.
(1)求X的分布及数学期望;
(2)若此时教室里有两扇或两扇以上的窗户被关闭,班长就会将关闭的窗户全部敞开,否则维持原状不变.记每天上午第三节课上课时该教室里敞开的窗户个数为Y,求Y的数学期望.