设抛物线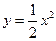 的焦点为F,准线为
的焦点为F,准线为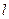 ,过点F作一直线与抛物线交于A、B两点,再分别过点A、B作抛物线的切线,这两条切线的交点记为P.
,过点F作一直线与抛物线交于A、B两点,再分别过点A、B作抛物线的切线,这两条切线的交点记为P.
(1)证明:直线PA与PB相互垂直,且点P在准线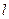 上;
上;
(2)是否存在常数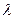 ,使等式
,使等式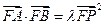 恒成立?若存在,求出
恒成立?若存在,求出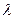 的值;若不存在,说明理由.
的值;若不存在,说明理由.
(本小题满分14分)
已知直线l与椭圆 (a>b>0)相交于不同两点A、B,
(a>b>0)相交于不同两点A、B, ,且
,且 ,以M为焦点,以椭圆的右准线为相应准线的双曲线与直线l相交于N(4,
,以M为焦点,以椭圆的右准线为相应准线的双曲线与直线l相交于N(4, 1). (I)求椭圆的离心率
1). (I)求椭圆的离心率 ; (II)设双曲线的离心率为
; (II)设双曲线的离心率为 ,记
,记 ,求
,求 的解析式,并求其定义域和值域.
的解析式,并求其定义域和值域.
(本小题满分12分)已知函数 ,
, .
.
(I)证明:当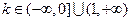 时,函数
时,函数 在其定义域内为单调函数;(II)若函数
在其定义域内为单调函数;(II)若函数 的图象在点(1,
的图象在点(1, )处的切线斜率为0,且当
)处的切线斜率为0,且当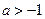 时,
时, ≥
≥ 在
在 上恒成立,求实数a的取值范围.
上恒成立,求实数a的取值范围.
(本小题满分12分)在长方体ABCD—A1B1C1D1中,AA1=1,AD=DC= .(1)求直线A1C与D1C1所成角的正切值;(2)在线段A1C上有一点Q,且C1Q=
.(1)求直线A1C与D1C1所成角的正切值;(2)在线段A1C上有一点Q,且C1Q= C1A1,求平面QDC与平面A1DC所成锐二面角的大小.
C1A1,求平面QDC与平面A1DC所成锐二面角的大小.
(本小题满分12分)某休闲会馆拟举行“五一”应祝活动,每位来宾交30元的入场费,可参加一次抽奖活动. 抽奖活动规则是:从一个装有分值分别为1,2,3,4,5,6的六个相同小球的抽奖箱中,有放回的抽取两次,每次抽取一个球,规定:若抽得两球的分值和为12分,则获得价值为m元的礼品;若抽得两球的分值和为11分或10分,则获得价值为100元的礼品;若抽得两球的分值和低于10分,则不获奖.(1)求每位会员获奖的概率;(2)假设会馆这次活动打算即不赔钱也不赚钱,则m应为多少元?
(本小题满分12分)
已知B ,C分别为 函数y=Asinωx  在y轴右侧的第一个最大值点和最小值点,O为原点,若
在y轴右侧的第一个最大值点和最小值点,O为原点,若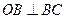 ,且
,且 (1) 求A ,ω 的值 (2)求函数y=Asinωx 的单调递增区间
(1) 求A ,ω 的值 (2)求函数y=Asinωx 的单调递增区间