(本小题满分12分)
下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量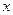 (吨)与相应的生产能耗
(吨)与相应的生产能耗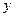 (吨标准煤)的几组对照数据
(吨标准煤)的几组对照数据
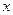 |
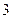 |
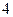 |
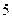 |
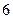 |
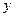 |
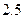 |
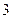 |
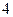 |
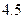 |
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出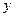 关于
关于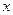 的线性回归方程
的线性回归方程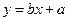 ;
;
(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(2)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤? (参考数值:
(参考数值: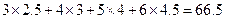 ,
,
(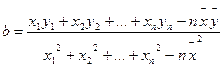 ,
,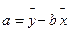 )
)
(本小题满分12分)如图,已知四棱锥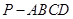 的底面为菱形,
的底面为菱形,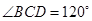 ,
, ,
,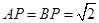 .
.

(Ⅰ)求证:AB⊥PC;
(Ⅱ)求点 到平面
到平面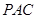 的距离.
的距离.
(本小题满分12分)某校团委会组织该校高中一年级某班以小组为单位利用周末时间进行了一次社会实践活动,且每个小组有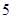 名同学,在实践活动结束后,学校团委会对该班的所有同学都进行了测评,该班的
名同学,在实践活动结束后,学校团委会对该班的所有同学都进行了测评,该班的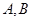 两个小组所有同学所得分数(百分制)的茎叶图如图所示,其中
两个小组所有同学所得分数(百分制)的茎叶图如图所示,其中 组一同学的分数已被污损,但知道
组一同学的分数已被污损,但知道 组学生的平均分比
组学生的平均分比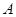 组学生的平均分高
组学生的平均分高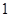 分.
分.
(Ⅰ)若在 组学生中随机挑选
组学生中随机挑选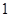 人,求其得分超过
人,求其得分超过 分的概率;
分的概率;
(Ⅱ)现从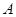 组这
组这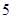 名学生中随机抽取
名学生中随机抽取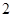 名同学,设其分数分别为
名同学,设其分数分别为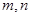 ,求
,求 的概率.
的概率.
(本小题满分12分)已知等差数列 的首项
的首项 ,公差
,公差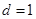 ,前
,前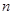 项和为
项和为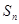 ,
, ,
,
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设数列 前
前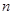 项和为
项和为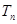 ,求
,求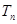
(本小题满分10分) 选修4—5:不等式选讲已知关于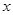 的不等式
的不等式 ,其解集为
,其解集为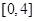 .
.
(Ⅰ)求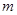 的值;
的值;
(Ⅱ)若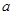 ,
, 均为正实数,且满足
均为正实数,且满足 ,求
,求 的最小值.
的最小值.
(本小题满分10分) 选修4—4:坐标系与参数方程
已知极坐标系的极点在直角坐标系的原点处,极轴与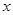 轴的正半轴重合,直线
轴的正半轴重合,直线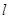 的极坐标方程为:
的极坐标方程为: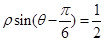 ,曲线
,曲线 的参数方程为:
的参数方程为:
(Ⅰ)写出直线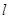 的直角坐标方程;
的直角坐标方程;
(Ⅱ)求曲线 上的点到直线
上的点到直线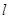 的距离的最大值.
的距离的最大值.