如图,棱锥P—ABCD的底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,BD=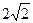 .
.
(Ⅰ)求证:BD⊥平面PAC;
(Ⅱ)求二面角P—CD—B的大小;
(Ⅲ)求点C到平面PBD的距离. 
(本小题满分13分)
已知数列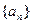 ,其前
,其前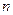 项和为
项和为 .
.
(1)求数列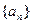 的通项公式,并证明数列
的通项公式,并证明数列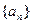 是等差数列;
是等差数列;
(2)如果数列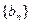 满足
满足 ,请证明数列
,请证明数列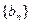 是等比数列;
是等比数列;
(3)设 ,数列
,数列 的前
的前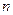 项和为
项和为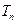 ,求使不等式
,求使不等式 对一切
对一切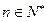 都成立的最大正整数
都成立的最大正整数 的值.
的值.
(本小题满分12分)
已知平面向量 ,
, ,函数
,函数 .
.
(1)写出函数 的单调递减区间;
的单调递减区间;
(2)设 ,求直线
,求直线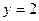
 与
与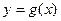 在闭区间
在闭区间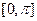 上的图像的所有交点坐标.
上的图像的所有交点坐标.
(本小题满分12分)
在△ABC中,设内角A、B、C的对边分别为a、b、c,
(Ⅰ)求角C的大小;
(Ⅱ)若 且
且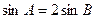 ,求
,求 的面积.
的面积.
(本小题满分12分)
设函数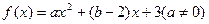 ,若不等式
,若不等式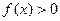 的解集为
的解集为 。
。
(1)求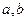 的值;
的值;
(2)若函数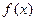 在
在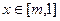
 上的最小值为1,求实数
上的最小值为1,求实数 的值。
的值。
(本小题满分12分)
已知两直线 .试确定
.试确定
 的值,使
的值,使
(1) //
//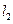 ;
;
(2)

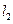 ,且
,且 在
在 轴上的
轴上的 截距为
截距为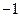 .
.