如图,已知△ABC中,AB=12,BC=8,AC=6,点D、E分别在AB、AC上,如果以A、D、E为顶点的三角形和以A、B、C为顶点的三角形相似,且相似比为 .
.
(1)根据题意确定D、E的位置,画出简图;
(2)求AD、AE和DE的长.
如图, 为 的直径, 为 上的一点, , , 的延长线交 于点 ,连接 .
(1)求证: 是 的切线;
(2)若 为 的中点,求 的值.

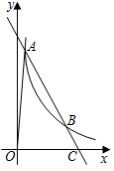
如图,已知一次函数 的图象与反比例函数 的图象交于点 和点 ,与 轴交于点 .
(1)分别求一次函数和反比例函数的解析式:
(2)求 的面积.
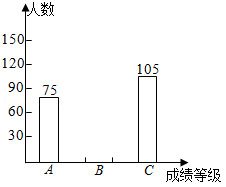
某校开展了“我爱古诗词”知识竞赛活动,将某年级参赛学生的成绩划分为三个等级进行统计分析,绘制得到如图表.
|
成绩等级 |
频数 |
频率 |
|
|
75 |
|
|
|
|
0.4 |
|
|
105 |
0.35 |
请结合图表信息,解答下列问题:
(1)该年级学生共有多少人?
(2)求表中 , 的值,并补全条形统计图;
(3)学校决定从参赛的甲、乙、丙、丁四名同学中任意抽取两名同学做经验介绍,求恰好选中甲、乙两位同学的概率.
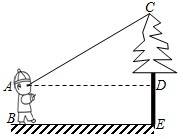
小丽用两锐角分别为 和 的三角尺测量一棵树的高度.如图,已知 , , ,那么这棵树大约有多高?(结果精确到 ,
已知关于 的一元二次方程 有两个不相等的实数根,求 的取值范围.