已知:某租赁公司出租同一型号的设备40套,当每套月租金为270元时,恰好全部租出。在此基础上,每套月租金每增加10元,就少租出1套设备。而未租出的设备每月需支付各种费用每套20元。
设每套设备实际月租金为x元(x≥270元),月收益为y元(总收益=设备租金收入-未租出设备费用)
问题1: 求y与x的二次函数关系式
问题2: 当x为何值时,月收益最大?最大值是多少?
问题3: 当月租金分别为300元/每套和350元/每套时,月收益各是多少?根据月收益的计算结果,此时公司应该选择出租多少套设备更合适,请简要说明理
如图,点D,E在△ABC的边BC上,连接AD,AE.①AB=AC;②AD=AE;③BD=CE.以此三个等式中的两个作为命题的题设,另一个作为命题的结论,构成三个命题:①②⇒③:①③⇒②;②③⇒①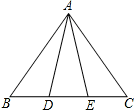
(1)以上三个命题是真命题的为(直接作答);
(2)请选择一个真命题进行证明(先写出所选命题,然后证明).
如图,五边形ABCDE中,BC=DE,AE=DC,∠C=∠E,DM⊥AB于M,试说明M是AB中点.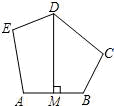
已知△ABC中∠BAC=140°,AB、AC的垂直平分线分别交BC于E、F.求∠EAF的度数.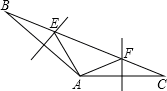
已知:如图,锐角△ABC的两条高BD、CE相交于点O,且OB=OC.试说明△ABC是等腰三角形.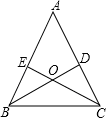
如图,点A、F、C、D在同一直线上,点B和点E分别在直线AD的两侧,且AB=DE,∠A=∠D,AF=DC.求证:BC∥EF.