(1)(本小题满分7分)选修4—2:矩阵与变换
已知二阶矩阵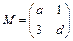 有特征值
有特征值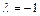 及对应的一个特征向量
及对应的一个特征向量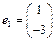 .
.
(Ⅰ)求矩阵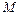 ;
;
(Ⅱ)设曲线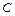 在矩阵
在矩阵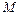 的作用下得到的方程为
的作用下得到的方程为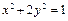 ,求曲线
,求曲线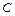 的方程.
的方程.
A是△BCD平面外的一点,E,F分别是BC,AD的中点.
(1)求证:直线EF与BD是异面直线;
(2)若AC⊥BD,AC=BD,求EF与BD所成的角.
如图所示,在边长为5+ 的长方形ABCD中,以A为圆心画一个扇形,以O为圆心画一个圆,M,N,K为切点,以扇形为圆锥的侧面,以圆O为圆锥底面,围成一个圆锥,求圆锥的全面积与体积.
的长方形ABCD中,以A为圆心画一个扇形,以O为圆心画一个圆,M,N,K为切点,以扇形为圆锥的侧面,以圆O为圆锥底面,围成一个圆锥,求圆锥的全面积与体积.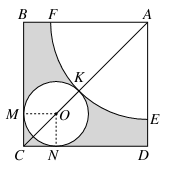
一个多面体的直观图及三视图如图所示:(其中M、N分别是AF、BC的中点)
(1)求证:MN∥平面CDEF;
(2)求多面体A-CDEF的体积.
已知正三棱锥V-ABC的正视图、侧视图和俯视图如图所示.
(1)画出该三棱锥的直观图;
(2)求出侧视图的面积.
已知某几何体的俯视图是如图所示的矩形,正视图是一个底边长为8,高为4的等腰三角形,侧视图(或称左视图)是一个底边长为6,高为4的等腰三角形.
(1)求该几何体的体积V;
(2)求该几何体的侧面积S.