如图所示,在边长为5+ 的长方形ABCD中,以A为圆心画一个扇形,以O为圆心画一个圆,M,N,K为切点,以扇形为圆锥的侧面,以圆O为圆锥底面,围成一个圆锥,求圆锥的全面积与体积.
的长方形ABCD中,以A为圆心画一个扇形,以O为圆心画一个圆,M,N,K为切点,以扇形为圆锥的侧面,以圆O为圆锥底面,围成一个圆锥,求圆锥的全面积与体积.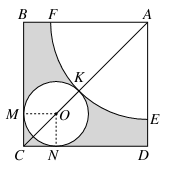
如图,已知椭圆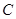 :
: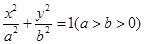 的离心率为
的离心率为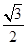 ,以椭圆
,以椭圆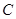 的左顶点
的左顶点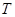 为圆心作圆
为圆心作圆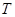 :
: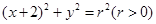 ,设圆
,设圆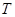 与椭圆
与椭圆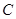 交于点
交于点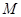 与点
与点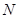 .
.
(1)求椭圆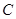 的方程;
的方程;
(2)求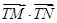 的最小值,并求此时圆
的最小值,并求此时圆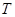 的方程;
的方程;
(3)设点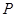 是椭圆
是椭圆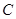 上异于
上异于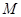 ,
,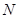 的任意一点,且直线
的任意一点,且直线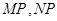 分别与
分别与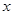 轴交于点
轴交于点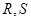 ,
, 为坐标原点,
为坐标原点,
求证: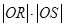 为定值.
为定值.
设 为数列
为数列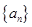 的前
的前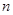 项和,对任意的
项和,对任意的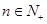 ,都有
,都有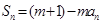 (
(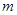 为正常数).
为正常数).
(1)求证:数列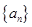 是等比数列;
是等比数列;
(2)数列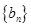 满足
满足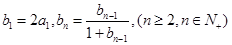 求数列
求数列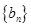 的通项公式;
的通项公式;
(3)在满足(2)的条件下,求数列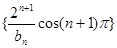 的前
的前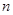 项和
项和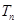 .
.
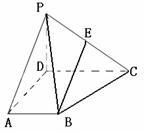
在四棱锥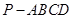 中,侧面
中,侧面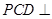 底面
底面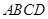 ,
,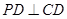 ,
,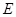 为
为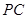 中点,底面
中点,底面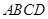 是直角梯形,
是直角梯形,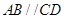 ,
,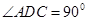 ,
,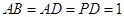 ,
,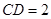 .
.
(1)求证: 面
面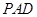 ;
;
(2)求证:面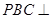 面
面 ;
;
(3)设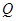 为棱
为棱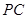 上一点,
上一点,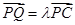 ,试确定
,试确定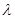 的值使得二面角
的值使得二面角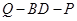 为
为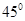 .
.
PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可 入肺颗粒物。我国PM2.5标准采用世卫组织设定的最宽限值,即PM2.5日均值在35微克/立方米以下空气质量为一级;在35微克/立方米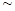 75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标.
75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标.
某试点城市环保局从该市市区2011年全年每天的PM2.5监测数据中随机的抽取15天的数据作为样本,监测值如茎叶图所示(十位为茎,个位为叶)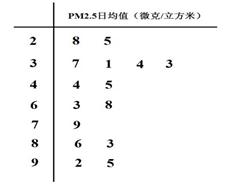
(I)从这15天的PM2.5日均监测数据中,随机抽出三天,求恰有一天空气质量达到一级的概率;
(II)从这15天的数据中任取三天数据,记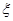 表示抽到PM2.5监测数据超标的天数,求
表示抽到PM2.5监测数据超标的天数,求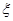 的分布列;
的分布列;
(III)以这15天的PM2.5日均值来估计一年的空气质量情况,则一年(按360天计算)中平均有多少天的空气质量达到一级或二级.
已知函数 ,
, 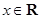 .
.
(1)求函数 的最大值和最小值;
的最大值和最小值;
(2)设函数 在
在 上的图象与
上的图象与 轴的交点从左到右分别为
轴的交点从左到右分别为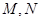 ,图象的最高点为
,图象的最高点为 ,
,
求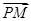 与
与 的夹角的余弦.
的夹角的余弦.