如图所示，两平行金属板A、B长度l=0.8m，间距d=0.6m．直流电源E能提供的最大电压为9×105V，位于极板左侧中央的粒子源可以沿水平方向向右连续发射比荷为=
l×107C/kg、重力不计的带电粒子，射人板间的粒子速度均为v0=4×106
m/s．在极板右侧有一个垂直纸面向里的匀强磁场，磁感应强度B=lT，分布在环带区域中，该环带的内外圆的圆心与两板间的中心重合于O点，环带的内圆半径Rl=
m．将变阻器滑动头由a向b慢慢滑动，改变两板间的电压时，带电粒子均能从不同位置穿出极板射向右侧磁场，且两板间电压最大时，对应的粒子恰能从极板右侧边缘穿出．
(1)问从板间右侧射出的粒子速度的最大值vm是多少?
(2)若粒子射出电场时，速度的反向延长线与v0所在直线交于O/点，试用偏转运动相关量证明O/点与极板右端边缘的水平距离x=
，即O/与0重合，所有粒子都好像从两板的中心射 出一样．
(3)为使粒子不从磁场右侧穿出，求环带磁场的最
小宽度d.
一艘客轮因故障需迅速组织乘客撤离。乘客在甲板上须利用固定的绳索下滑到救援快艇上。绳索与竖直方向的夹角θ＝37°，设乘客下滑过程绳索始终保持直线。为保证行动又快又安全，乘客先从静止开始匀加速滑到某最大速度，再匀减速滑至快艇，速度刚好为零，加速过程与减速过程中的加速度大小相等。在乘客开始下滑时，船员同时以水平速度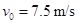
向快艇抛出救生圈刚好落到救援快艇上（快艇可视为质点），如图所示。并知乘客下滑的时间是救生圈平抛下落的2倍，不计空气阻力，重力加速度g取10 m/s2，sin37°= 0.6，cos37°= 0.8，求：
（1）乘客沿着绳索下滑的时间t；
（2）乘客下滑过程的最大速度vm。
如图所示，在光滑的水平面上有一质量为m=1kg的足够长的木板C，在C上放置有A、B两物体，A的质量mA=1kg，B的质量为mB=2kg．A、B之间锁定一被压缩了的轻弹簧，弹簧储存的弹性势能Ep=3J，现突然给A、B一瞬时冲量作用，使A、B同时获得v0=2m/s的初速度，且同时弹簧由于受到扰动而解除锁定，并在极短的时间内恢复原长，之后与A、B分离．已知A和C之间的摩擦因数为μ1=0.2，B、C之间的动摩擦因数为μ2=0.1，且滑动摩擦力略小于最大静摩擦力．求：
（1）弹簧与A、B分离的瞬间，A、B的速度分别是多大？
（2）已知在C第一次碰到右边的固定挡板之前，A、B和C已经达到了共同速度，求在到达共同速度之前A、B、C的加速度分别是多大及该过程中产生的内能为多少？
（3）已知C与挡板的碰撞的碰撞无机械能损失，求在第一次碰撞后到第二次碰撞前A在C上滑行的距离？
如图所示，区域Ⅰ中有竖直向上的均强电场，电场强度为E；区域Ⅱ内有垂直纸面向外的水平均强磁场，磁感应强度为B；区域Ⅲ中有垂直纸面向里的水平均强磁场，磁感应强度为2B．一质量为m、带电量为q的带负电粒子（不计重力）从左边界O点正上方的M点以速度v0水平射入电场，经水平分界线OP上的A点与OP成60°角射入Ⅱ区域的磁场，并垂直竖直边界CD进入Ⅲ区域的均强磁场中．求：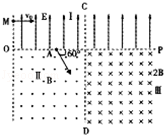
（1）粒子在Ⅱ区域匀强磁场中运动的轨道半径；
（2）O、M间的距离；
（3）粒子从第一次进入区域Ⅱ到第一次离开区域Ⅲ所经历的时间t．
如图，将质量m=1kg的圆环套在固定的倾斜直杆上，杆的倾角为37°，环的直径略大于杆的截面直径．对环施加一位于竖直平面内斜向上与杆夹角为37°的拉力F=10N，使圆环由静止开始沿杆加速度向上运动，已知环与杆间动摩擦因数μ=0.5．（g取10m/s2）求：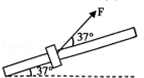
（1）F作用2s时圆环的速度是多大？
（2）2s后撤去力F，求圆环继续沿杆上滑的最大距离是多少？
“重力探矿”是常用的探测石油矿藏的方法之一。其原理可简述如下：如图，P、Q为某地区水平地面上的两点，在P点正下方一球形区域内储藏有石油，假定区域周围岩石均匀分布，密度为
；石油密度远小于，可将上述球形区域视为空腔。如果没有这一空腔，则该地区重力加速度（正常值）沿竖直方向；当存在空腔时，该地区重力加速度的大小和方向会与正常情况有微小偏差。重力加速度在原坚直方向（即PO方向）上的投影相对于正常值的偏离叫做“重力加速度反常”。为了探寻石油区域的位置和石油储量，常利用P点附近重力加速度反常现象。已知引力常数为G。
（1）“重力探矿”利用了“割补法”原理：如图所示，在一个半径为R、质量为M的均匀球体中，紧贴球的边缘挖去一个半径为R/2的球形空穴后，剩余的阴影部分对位于球心和空穴中心连线上、与球心相距d的质点m的引力是多大?
（2）设球形空腔体积为V，球心深度为d（远小于地球半径），
=x，利用“割补法”原理：如果将近地表的球形空腔填满密度为的岩石,则该地区重力加速度便回到正常值.因此,重力加速度反常值可通过填充后的球形区域对Q处物体m产生的附加引力
来计算,式中M是填充岩石后球形区域的质量,求空腔所引起的Q点处的重力加速度反常值
（
在OP方向上的分量）
（3）若在水平地面上半径L的范围内发现：重力加速度反常值在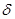
与
（k>1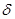）（为常数）之间变化，且重力加速度反常的最大值出现在半为L的范围的中心,如果这种反常是由于地下存在某一球形空腔造成的，试求此球形空腔球心的深度和空腔的体积。