如图,长方体 中,
中, ,
, ,点
,点 为
为 的中点.
的中点.
(1)求证:直线 ∥平面
∥平面 ;
;
(2)求证:平面
 平面
平面 ;
;
(3)求 与平面
与平面 所成的角大小.
所成的角大小.
设函数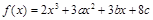 在
在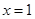 及
及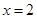 时取得极值.
时取得极值.
(1)求a、b的值;
(2)若对于任意的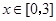 ,都有
,都有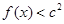 成立,求c的取值范围.
成立,求c的取值范围.
已知函数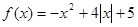 .
.
(1)画出函数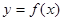 在闭区间
在闭区间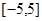 上的大致图像;
上的大致图像;
(2)若直线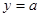 与
与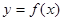 的图像有2个不同的交点,求实数
的图像有2个不同的交点,求实数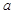 的取值范围.
的取值范围.
在交通拥挤地段,为了确保交通安全,规定机动车相互之间的距离d(米)与车
速v(千米/小时)需遵循的关系是 (其中a(米)是车身长,a为常量),同时
(其中a(米)是车身长,a为常量),同时
规定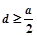 .
.
(1)当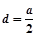 时,求机动车车速的变化范围;
时,求机动车车速的变化范围;
(2)设机动车每小时流量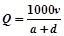 ,应规定怎样的车速,使机动车每小时流量Q最大.
,应规定怎样的车速,使机动车每小时流量Q最大.
在直角坐标系中,曲线C1的参数方程为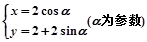 ,M是曲线C1上
,M是曲线C1上
的动点,点P满足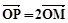
(1)求点P的轨迹方程C2;
(2)以O为极点,x轴正半轴为极轴的极坐标系中,射线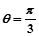 与曲线C1、C2交于不同于极点的A、B两点,求|AB|.
与曲线C1、C2交于不同于极点的A、B两点,求|AB|.
已知函数
(1)当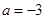 时,求不等式
时,求不等式 的解集;
的解集;
(2)若 的解集包含
的解集包含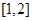 ,求
,求 的取值范围.
的取值范围.