两质量分别为M1和M2的劈A和B,高度相同,放在光滑水平面上,A和B的倾斜面都是光滑曲面,曲面下端与水平面相切,如图所示,一质量为m的物块位于劈A的倾斜面上,距水平面的高度为h。物块从静止滑下,然后又滑上劈B。求物块在B上能够达到的最大高度。
(18分)如图所示,长为L的不可伸长的绳子一端固定在O点,另一端系质量为m的小球,小球静止在光滑水平面上。现用大小为F水平恒力作用在另一质量为2m的物块上,使其从静止开始向右运动,一段时间后撤去该力,物块与小球发生正碰后速度大小变为原来的一半而速度方向不变,小球恰好能在竖直平面内做圆周运动。已知重力加速度为g,小球和物体均可视为质点,试求: 
(1)小物块碰撞前速度V0的大小;
(2)碰撞过程中系统损失的机械能;
(3)恒力F作用时间。
如图,一滑块通过长度不计的短绳拴在小车的板壁上,小车上表面光滑。小车由静止开始向右匀加速运动,经过2s,细绳断裂。细绳断裂后,小车的加速度不变,又经过一段时间,滑块从小车左端刚好掉下,在这段时间内,已知滑块相对小车前3s内滑行了4.5m,后3s内滑行了10.5m。求: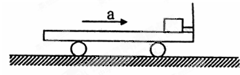
(1)小车底板长是多少?
(2)从小车开始运动到滑块离开车尾,滑块相对于地面移动的距离是多少?
如图所示,一条上端固定的绳长l1=7.5m,质量m=60Kg的特技演员从绳上端先沿绳从静止开始无摩擦下滑一段距离后,突然握紧绳子,与绳子之间产生f="1800" N的摩擦阻力。滑到绳子末端时速度刚好为零。求:
(1)特技演员下滑所用的时间t.
(2)在水平面上有一辆长l2=3m平板车,其上表面与绳末端等高,车右端离绳末端s=4m,平板车能一直以v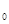 ="2" m/s的恒定速度向右运动,为了要让该演员滑下后能留在车上,则车启动后演员应在多长时间范围内开始下滑?(把人看作质点,人与车之间动摩擦系数μ=0.2, g取10m/s2)
="2" m/s的恒定速度向右运动,为了要让该演员滑下后能留在车上,则车启动后演员应在多长时间范围内开始下滑?(把人看作质点,人与车之间动摩擦系数μ=0.2, g取10m/s2)
为了体现人文关怀,保障市民出行安全和严格执法,各大都市市交管部门强行推出了“电子眼”,据了解,在城区内全方位装上“电子眼”后立马见效,机动车擅自闯红灯的大幅度减少,因闯红灯引发的交通事故也从过去的5%下降到1%。现有甲、乙两汽车正沿同一平直马路同向匀速行驶,甲车在前,乙车在后,它们行驶的速度均为10m/s.当两车快要到一十字路口时,甲车司机看到绿灯已转换成了黄灯,于是紧急刹车(反应时间忽略不计),乙车司机为了避免与甲车相撞也紧急刹车,但乙车司机反应较慢(反应时间为0.5s)。已知甲车紧急刹车时制动力为车重的0.4倍,乙车紧急刹车制动力为车重的0.5倍,求:
(1)若甲司机看到黄灯时车头距警戒线15m,他采取上述措施能否避免闯红灯?
(2)为保证两车在紧急刹车过程中不相撞,甲、乙两车行驶过程中应保持多大距离?
如图所示是一种研究劈的作用的装置,托盘A固定在细杆上,细杆放在固定的圆孔中,下端有滚轮,细杆只能在竖直方向上移动,在与托盘连接的滚轮正下面的底座上也固定一个滚轮,轻质劈放在两滚轮之间,劈背的宽度为a,侧面的长度为l,劈尖上固定的细线通过滑轮悬挂总质量为m的钩码,调整托盘上所放砝码的质量M,可以使劈在任何位置时都不发生移动.忽略一切摩擦和劈、托盘、细杆与滚轮的重力,若a=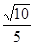 l,试求M是m的多少倍?
l,试求M是m的多少倍?