((本题16分)
已知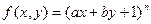 (常数
(常数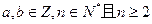 )
)
(1)若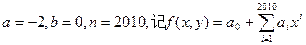 求:①
求:①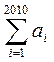 ;②
;②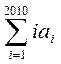
(2)若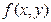 展开式中不含x的项的系数的绝对值之和为729,不含y项的系数的绝对值之和为64,求n的所有可能值。
展开式中不含x的项的系数的绝对值之和为729,不含y项的系数的绝对值之和为64,求n的所有可能值。
如图,四棱锥P—ABCD的底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点.
(1)求异面直线PA与DE所成角的大小;
(2)求二面角B—DE—C的平面角的余弦值;
(3)在棱PB上是否存在点F,使PB⊥平面DEF?证明你的结论.
如图, 在直三棱柱 中,
中, ,
, ,点
,点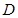 是
是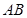 的中点,
的中点,
(1)求证: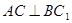 ;
;
(2)求证: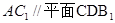 ;
;
(3)求直线 与平面
与平面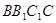 所成角的正切值.
所成角的正切值.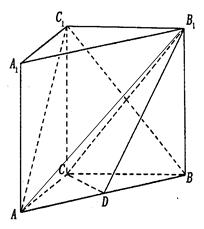
已知关于 的方程
的方程 .
.
(1)若方程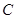 表示圆,求实数
表示圆,求实数 的取值范围 ;
的取值范围 ;
(2)若圆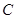 与直线
与直线 相交于
相交于 两点,且
两点,且 ,求
,求 的值
的值
已知向量
(1)求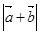 和
和 ;
;
(2) 为何值时,向量
为何值时,向量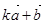 与
与 垂直;
垂直;
(3) 为何值时,向量
为何值时,向量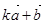 与
与 平行。
平行。
已知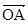 =(2asin2x,a),
=(2asin2x,a), =(-1,2
=(-1,2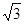 sinxcosx+1),O为坐标原点,a≠0,设f(x)=
sinxcosx+1),O为坐标原点,a≠0,设f(x)=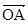 ·
· +b,b>a。
+b,b>a。
(1)若a>0,写出函数y=f(x)的单调递增区间;
(2)若函数y=f(x)的定义域为[ ,π],值域为[2,5],求实数a与b的值。
,π],值域为[2,5],求实数a与b的值。