（本小题满分12分）
为调查某市学生百米运动成绩,从该市学生中按照男女生比例随机抽取50名学生进行百米测试，学生成绩全部都介于13秒到18秒之间，将测试结果按如下方式分成五组，第一组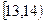
，第二组
……第五组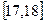
，如图是按上述分组方法
得到的频率分布直方图．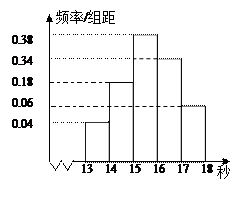
（Ⅰ）求这组数据的众数和中位数（精确到0．1）；
( II )根据有关规定，成绩小于16秒为达标．
(ⅰ)用样本估计总体，某班有学生45人,设
为达标人数,求的数学期望与方差．
(ⅱ)如果男女生使用相同的达标标准,则男女
生达标情况如下表
| 性别 是否达标 |
男 |
女 |
合计 |
| 达标 |
 |
 ______ |
_____ |
| 不达标 |
 _____ |
 |
_____ |
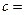| 合计 |
______ |
______ |
 |
根据上表数据，能否有99%的把握认为“体育达标与性别有关”？若有，你能否提出一个更好的解决方法来？
（m＞n＞0)，求θ的其他三角函数值.
