(本小题满分10分)选修4—5:不等式选讲
设 (
(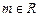 ).
).
(Ⅰ)当 时,求函数
时,求函数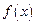 的定义域;
的定义域;
(Ⅱ)若当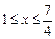 时,
时,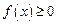 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
设函数 处的切线与直线
处的切线与直线 平行.
平行.
(1)求 的值;
的值;
(2)求函数 在区间[0,1]的最小值;
在区间[0,1]的最小值;
(3)若 ,根据上述(I)
,根据上述(I) 、(II)的结论,证明:
、(II)的结论,证明:
(1)已知 是正常数,
是正常数, ,
, ,求证:
,求证: ,指出等号成立的条件;
,指出等号成立的条件;
(2)利用(1)的结论求函数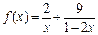 (
(
 )的最小值,并指出取最小值时
)的最小值,并指出取最小值时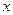 的值.
的值.
某地政府为科技兴市,欲将如图所示的一块不规则的非农业用地规划建成一个矩形的高科技工业园区.已知 ⊥
⊥ ,
,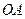 ∥
∥ ,且
,且 ,
,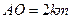 ,
, 曲线段
曲线段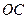 是以点
是以点 为顶
为顶 点且开口向上的抛物线的一段.如果要使矩形的相邻两边分别落
点且开口向上的抛物线的一段.如果要使矩形的相邻两边分别落
在 ,
, 上,且一个顶点落在曲线段
上,且一个顶点落在曲线段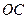 上.问:应如何规划才能使矩形工业园区的用地面积最大?并求出最大的用地面积(精确到
上.问:应如何规划才能使矩形工业园区的用地面积最大?并求出最大的用地面积(精确到 ).
).
已知抛物线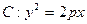 ,点
,点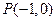 是其准线与
是其准线与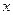 轴的焦点,过
轴的焦点,过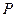 的直线
的直线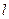 与抛物线
与抛物线 交于
交于 、
、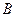 两点
两点 ,
, 为抛物线
为抛物线 的焦点.当线段
的焦点.当线段 的中点在直线
的中点在直线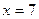 上时,求直线
上时,求直线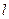 的方程,并求出此时
的方程,并求出此时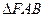 的面积.
的面积.
已知直线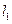 为曲线
为曲线 的切线,且与直线
的切线,且与直线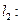
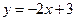 垂直.
垂直.
(1)求直线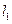 的方程;
的方程;
(2)求 由直线
由直线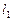 、
、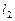 和
和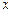 轴所围成的三角形
轴所围成的三角形 的面积.
的面积.