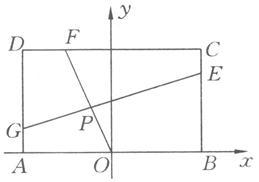
某地政府为科技兴市,欲将如图所示的一块不规则的非农业用地规划建成一个矩形的高科技工业园区.已知 ⊥
⊥ ,
,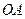 ∥
∥ ,且
,且 ,
,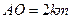 ,
, 曲线段
曲线段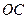 是以点
是以点 为顶
为顶 点且开口向上的抛物线的一段.如果要使矩形的相邻两边分别落
点且开口向上的抛物线的一段.如果要使矩形的相邻两边分别落
在 ,
, 上,且一个顶点落在曲线段
上,且一个顶点落在曲线段 上.问:应如何规划才能使矩形工业园区的用地面积最大?并求出最大的用地面积(精确到
上.问:应如何规划才能使矩形工业园区的用地面积最大?并求出最大的用地面积(精确到 ).
).
如果直线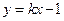 与双曲线
与双曲线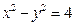 两支各有一个交点,求
两支各有一个交点,求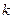 的取值范围.
的取值范围.
已知椭圆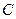 的中心在原点
的中心在原点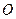 ,焦点在
,焦点在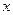 轴上,右准线的方程为
轴上,右准线的方程为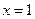 ,倾斜角为
,倾斜角为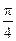 的直线
的直线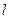 交椭圆
交椭圆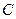 于
于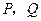 两点,且
两点,且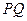 的中点坐标为
的中点坐标为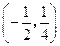 ,设
,设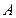 为椭圆
为椭圆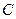 的右顶点,
的右顶点,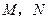 为椭圆
为椭圆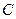 上两点,且
上两点,且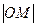 ,
,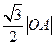 ,
,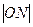 三者的平方成等差数列,则直线
三者的平方成等差数列,则直线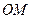 和
和 斜率之积的绝对值是否为定值,若是,请求出定值;若不是,请说明理由.
斜率之积的绝对值是否为定值,若是,请求出定值;若不是,请说明理由.
已知椭圆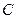 的中心在原点
的中心在原点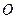 ,焦点在
,焦点在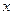 轴上,右准线的方程为
轴上,右准线的方程为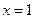 ,倾斜角为
,倾斜角为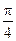 的直线
的直线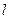 交椭圆
交椭圆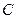 于
于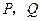 两点,且
两点,且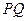 的中点坐标为
的中点坐标为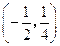 ,求椭圆
,求椭圆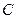 的方程;
的方程;
已知椭圆的中心为坐标原点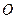 ,焦点在
,焦点在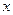 轴上,斜率为
轴上,斜率为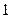 且过椭圆右焦点
且过椭圆右焦点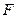 的直线交椭圆于
的直线交椭圆于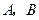 两点,
两点,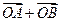 与
与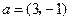 共线.设
共线.设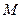 为椭圆上任意一点,且
为椭圆上任意一点,且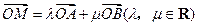 ,证明
,证明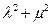 为定值.
为定值.
已知常数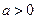 ,在矩形
,在矩形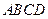 中,
中,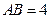 ,
,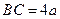 ,
,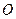 为
为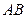 的中点.点
的中点.点 分别在
分别在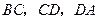 上移动,且
上移动,且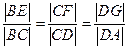 ,
,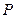 为
为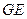 与
与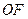 的交点(如图).问是否存在两个定点,使点
的交点(如图).问是否存在两个定点,使点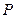 到这两点的距离的和为定值?若存在,求出这两点的坐标及此定值;若不存在,请说明理由.
到这两点的距离的和为定值?若存在,求出这两点的坐标及此定值;若不存在,请说明理由.