已知常数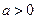 ,在矩形
,在矩形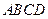 中,
中,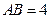 ,
,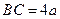 ,
,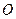 为
为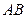 的中点.点
的中点.点 分别在
分别在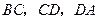 上移动,且
上移动,且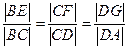 ,
,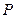 为
为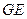 与
与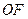 的交点(如图).问是否存在两个定点,使点
的交点(如图).问是否存在两个定点,使点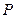 到这两点的距离的和为定值?若存在,求出这两点的坐标及此定值;若不存在,请说明理由.
到这两点的距离的和为定值?若存在,求出这两点的坐标及此定值;若不存在,请说明理由.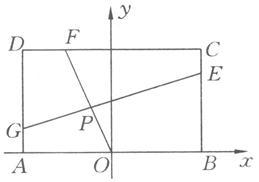
某工厂年初用98万元购买一台新设备,第一年设备维修及燃料、动力消耗(称为设备的低劣化)的总费用12万元,以后每年都增加4万元,新设备每年可给工厂收益50万元.
(Ⅰ)工厂第几年开始获利?
(Ⅱ)若干年后,该工厂有两种处理该设备的方案:①年平均获利最大时,以26万元出售该设备;②总纯收入获利最大时,以8万元出售该设备,问哪种方案对工厂合算?
已知函数 .
.
(Ⅰ)若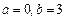 ,函数
,函数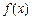 在
在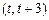 上既能取到极大值,又能取到极小值,求
上既能取到极大值,又能取到极小值,求 的取值范围;
的取值范围;
(Ⅱ)当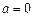 时,
时, 对
对 任意的
任意的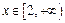 恒成立,求
恒成立,求 的取值范围.
的取值范围.
(本小题满分12分)
如图2,在直三棱柱ABC- 中,AB=1,
中,AB=1,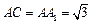 ,
,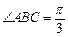 .
.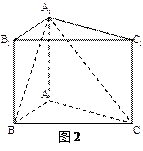
(Ⅰ)证明: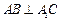 ;
;
(Ⅱ)求二面角 的正弦值.
的正弦值.
已知向量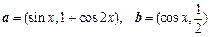 ,定义函数
,定义函数
(Ⅰ)求函数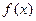 最小正周期;
最小正周期;
(Ⅱ)在△ABC中,角A为锐角,且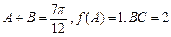 ,求边AC的长.
,求边AC的长.
四、附加题(本题满分10分,记入总分)
23..已知数列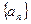 中,
中,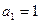 ,
,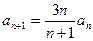 ,求
,求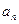 .
.