（本小题满分14分）
(1) 证明：当
时，不等式
成立；
(2) 要使上述不等式成立，能否将条件“”适当放宽？若能，请放宽条件并简述理由；若不能，也请说明理由；
(3)请你根据⑴、⑵的证明，试写出一个类似的更为一般的结论，且给予证明．
（本小题12分）
已知数列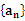
的前项和Sn，满足Sn2an2n （n
（1）求数列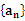的通项公式
（2）若数列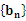
满足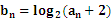
，Tn为数列
的前n项和，求证：Tn
（本小题12分）
在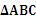
中，A,B,C的对边分别为a,b,c，且bcosC3acosBccosB
（1） 求cosB的值
（2） 若
求a和c边的长
（本小题12分）
已知函数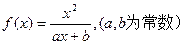
，且方程f（x）
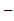x12=0有两个实根x13,x24
（1）求函数f（x）的解析式
（2）设k>1，解关于x的不等式f（x）<
（本小题10分）
已知两点A（0,1），B（2,m）， 如果经过A与B且与x轴相切的圆有且只有一个，求m的值及圆的方程。
（本题12分）已知函数
，
（1）若
，求
的单调区间；
（2）若
恒成立，求
的取值范围。