已知圆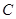 的圆心在坐标原点,且与直线
的圆心在坐标原点,且与直线 相切
相切
(1)求直线 被圆
被圆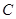 所截得的弦
所截得的弦 的长.
的长.
(2)过点 作两条与圆
作两条与圆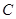 相切的直线,切点分别为
相切的直线,切点分别为 ,
, ,求直线
,求直线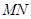 的方程
的方程
(3)若与直线 垂直的直线
垂直的直线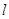 与圆
与圆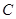 交于不同的两点
交于不同的两点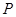 ,
, ,且
,且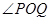 为钝角,求直线
为钝角,求直线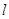 纵截距的取值范围.
纵截距的取值范围.
如图所示,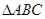 是等腰直角三角形,
是等腰直角三角形,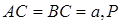 是
是 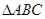 所在平面外一点,
所在平面外一点,
(1)求证:面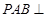 面
面 ;
;
(2)求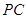 和
和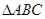 所在平面所成角。(本题12分)
所在平面所成角。(本题12分)
已知9个外语教师,4人只会英语,3人只会日语,另外2人既会英语又会日语,从中选4人,2人教英语,2人教日语,有多少种不同安排方案?(本题12分)
在空间四边形ABCD中,已知AC=2,BD=2,E、F分别为AD、BC中点,且EF=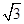 ,
,
求AC和BD所成的角。(本题12分)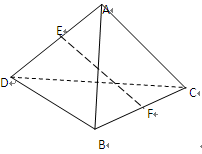
有5名男生,4名女生排成一排。(1)女生必须相邻,有多少种排法?(2)女生不能相邻,有多少种排法?(本题10分)
某市公用电话(市话)的收费标准为:3分钟之内(包括3分钟)收取0.30元/分钟;超过3分钟部分按0.10元/分钟收费。设计一个程序,根据通话时间计算话费,画出程序框图.