(本小题满分14分)
已知: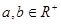 , 求证:
, 求证: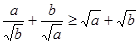 .
.
(本小题满分15分)
如图,设抛物线C: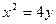 的焦点为F,
的焦点为F,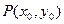 为抛物线上的任一点(其中
为抛物线上的任一点(其中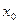 ≠0),[
≠0),[
过P点的切线交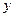 轴于Q点.
轴于Q点.
(Ⅰ)证明: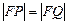 ;
;
(Ⅱ)Q点关于原点O的对称点为M,过M点作平行于PQ的直线
交抛物线C于A、B两点,若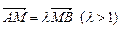 ,求
,求 的值.
的值.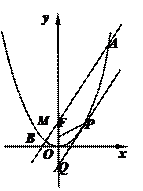
(本小题满分15分)
设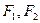 分别为椭圆
分别为椭圆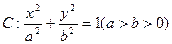 的左、右两个焦点.
的左、右两个焦点.
(Ⅰ)若椭圆 上的点
上的点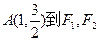 两点的距离之和等于4,
两点的距离之和等于4,
求椭圆 的方程和焦点坐标;
的方程和焦点坐标;
(Ⅱ)设点P是(Ⅰ)中所得椭圆上的动点,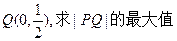 。
。
(15分) 如图,金砂公园有一块边长为2的等边△ABC的边角地,现修成草坪,图中DE把草坪
分成面积相等的两部分,D在AB上,E在AC上.
(Ⅰ)设AD= ,DE=
,DE= ,求
,求 关于
关于 的函数关系式;
的函数关系式;
(Ⅱ)如果DE是灌溉水管,我们希望它最短,则DE的位置应在哪里?请予以证明.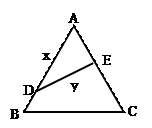
如图①在直角梯形ABCP中,BC∥AP,AB⊥BC,CD⊥AP,AD=DC=PD=2,E,F,G分别是线段PC、PD,BC的中点,现将ΔPDC折起,使平面PDC⊥平面ABCD(如图②)
(Ⅰ)求证AP∥平面EFG;
(Ⅱ)求二面角G-EF-D的大小;
(Ⅲ)在线段PB上确定一点Q,使PC⊥平面ADQ,试给出证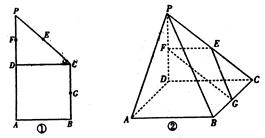 明.
明.
(本小题满分14)
设命题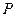 :
: ,命题
,命题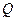 :
: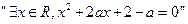 ;
;
如果“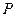 或
或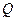 ”为真,“
”为真,“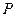 且
且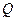 ”为假,求
”为假,求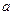 的取值范围。
的取值范围。