为了在夏季降温和冬季供暖时减少能源消耗,房屋的屋顶和外墙需要建造隔热层,某栋建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元.该建筑物每年的能源消耗费用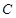 (单位:万元)与隔热层厚度
(单位:万元)与隔热层厚度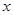 (单位:
(单位: )满足关系:
)满足关系:
若不建隔热层,每年能源消耗费用为8万元。设 为隔热层建造费用与20年的能源消耗费用之和。
为隔热层建造费用与20年的能源消耗费用之和。
(Ⅰ)求 的值及
的值及 的表达式;
的表达式;
(Ⅱ)隔热层修建多厚时,总费用 最小,并求最小值.
最小,并求最小值.
已知向量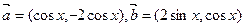 ,
,
(1)求函数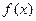 的最小正周期;
的最小正周期;
(2)若 ,求
,求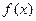 的最大值和最小值。
的最大值和最小值。
圆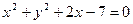 内一点
内一点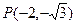 ,过点
,过点 的直线
的直线 的倾斜角为
的倾斜角为 ,直线
,直线 交圆于
交圆于 两点,
两点,
(1)当 时,求弦
时,求弦 的长;
的长;
(2)当弦 最短时,求直线
最短时,求直线 的方程。
的方程。
(本小题满分12分)
对于函数 ,若存在
,若存在 R,使
R,使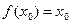 成立,则称
成立,则称 为
为 的不动点.如果函数
的不动点.如果函数 N*
N*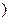 有且仅有两个不动点0和2,且
有且仅有两个不动点0和2,且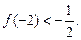
(1)求实数 ,
, 的值;
的值;
(2)已知各项不为零的数列
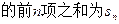 ,并且
,并且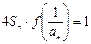 , 求数列
, 求数列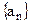 的通项公式;;
的通项公式;;
(3)求证: .
.
(本小题满分12分)
已知F1、F2分别是双曲线x2-y2=1的两个焦点,O为坐标原点,圆O是以F1F2为直径的圆,直线l:y=kx+b (b>0)与圆O相切,并与双曲线相交于A、B两点.
(1)根据条件求出b和k满足的关系式;
(2)向量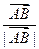 在向量
在向量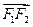 方向的投影是p,当(×)p2=1时,求直线l的方程;
方向的投影是p,当(×)p2=1时,求直线l的方程;
(3)当(× )p2=m且满足2≤m≤4时,求DAOB面积的取值范围.
)p2=m且满足2≤m≤4时,求DAOB面积的取值范围.
(本小题满分12分)
已知双曲线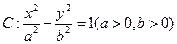 的离心率为
的离心率为 ,右准线方程为
,右准线方程为
(1)求双曲线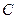 的方程;
的方程;
(2)设直线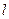 是圆
是圆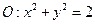 上动点
上动点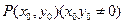 处的切线,
处的切线,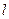 与双曲线
与双曲线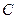 交于不同的两点
交于不同的两点 ,证明
,证明 的大小为定值.
的大小为定值.